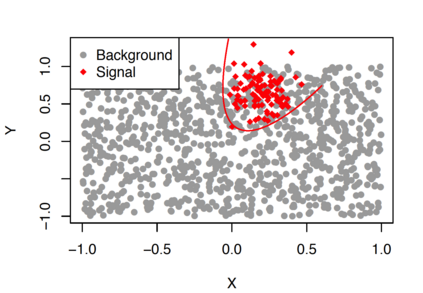
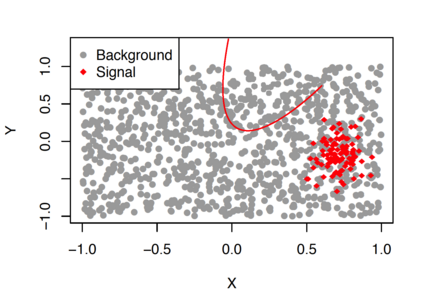
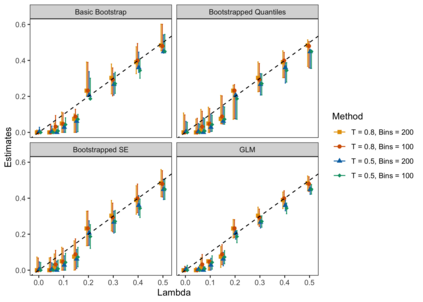
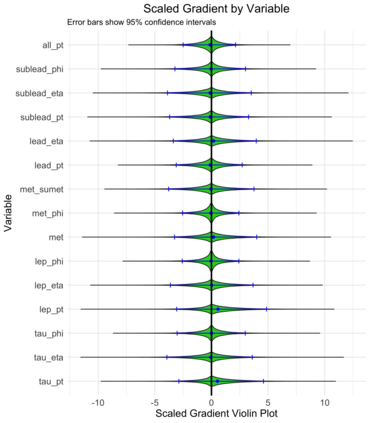
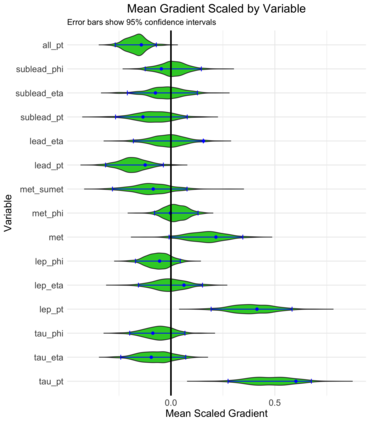
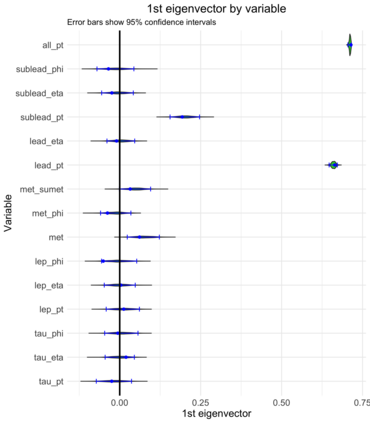
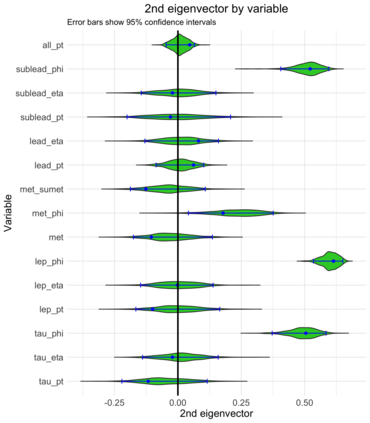
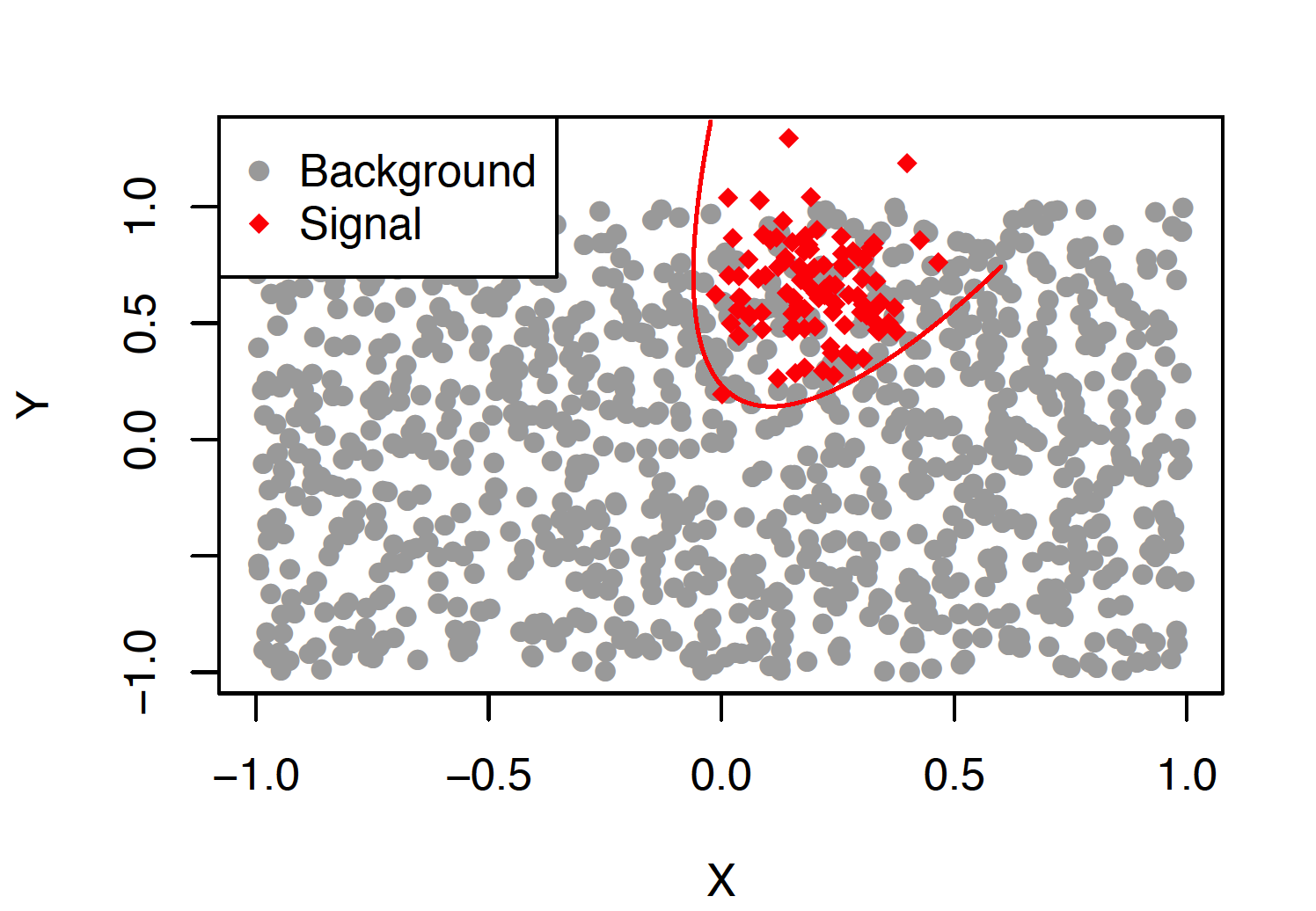
A central goal in experimental high energy physics is to detect new physics signals that are not explained by known physics. In this paper, we aim to search for new signals that appear as deviations from known Standard Model physics in high-dimensional particle physics data. To do this, we determine whether there is any statistically significant difference between the distribution of Standard Model background samples and the distribution of the experimental observations, which are a mixture of the background and a potential new signal. Traditionally, one also assumes access to a sample from a model for the hypothesized signal distribution. Here we instead investigate a model-independent method that does not make any assumptions about the signal and uses a semi-supervised classifier to detect the presence of the signal in the experimental data. We construct three test statistics using the classifier: an estimated likelihood ratio test (LRT) statistic, a test based on the area under the ROC curve (AUC), and a test based on the misclassification error (MCE). Additionally, we propose a method for estimating the signal strength parameter and explore active subspace methods to interpret the proposed semi-supervised classifier in order to understand the properties of the detected signal. We investigate the performance of the methods on a data set related to the search for the Higgs boson at the Large Hadron Collider at CERN. We demonstrate that the semi-supervised tests have power competitive with the classical supervised methods for a well-specified signal, but much higher power for an unexpected signal which might be entirely missed by the supervised tests.
翻译:实验性高能物理学的中心目标是检测已知物理学所没有解释的新的物理信号。 在本文中, 我们的目标是寻找在高度粒子物理数据中与已知的标准模型物理有偏差的新信号。 为此, 我们确定标准模型背景样本的分布和实验观测分布之间是否有统计上的重大差异, 它们是背景和潜在新信号的混合体。 传统上, 人们也可以从虚度信号分布模型中获取样本。 我们在这里调查一种模型独立的方法, 不对该信号作任何假设, 使用半监督的分类器来检测实验数据中存在的信号。 我们使用分类器构建三种测试统计数据: 估计概率比测试( LRT) 统计, 以ROC曲线下的区域为基础进行的测试, 以及基于错误分类错误( MCE) 的测试。 此外, 我们提出一种方法来估计信号强度参数, 并探索一种积极的亚空间方法, 来解释拟议的半监督式分类器, 以便完全了解实验性信号在实验数据中的存在。 我们用高压级C 测试方法来调查我们所检测的试测得的C 。