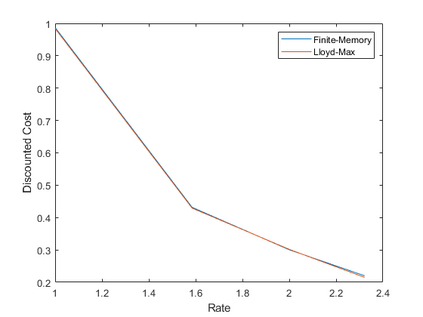
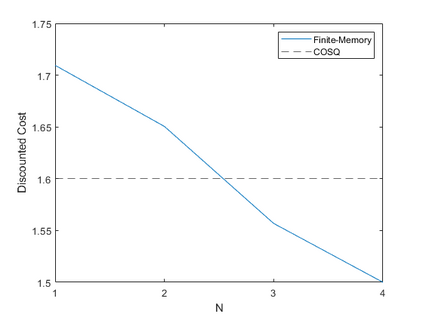
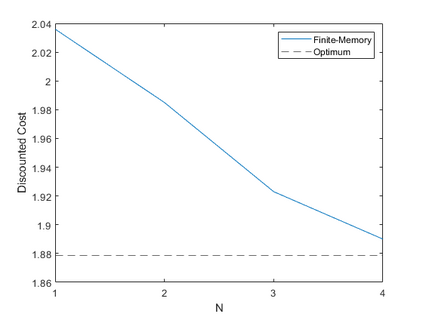
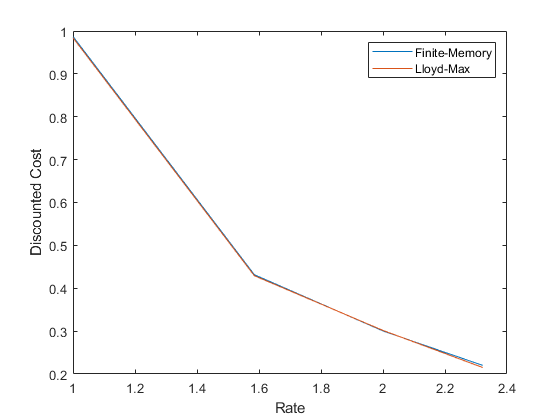
We study the problem of zero-delay coding of a Markov source over a noisy channel with feedback. We first formulate the problem as a Markov decision process (MDP) where the state is a previous belief term along with a finite memory of channel outputs and quantizers. We then approximate this state by marginalizing over all possible beliefs, so that our policies only use the finite-memory term to encode the source. Under an appropriate notion of predictor stability, we show that such policies are near-optimal for the zero-delay coding problem as the memory length increases. We also give sufficient conditions for predictor stability to hold, and propose a reinforcement learning algorithm to compute near-optimal finite-memory policies. These theoretical results are supported by simulations.
翻译:暂无翻译