A Unified Theory of Diversity in Ensemble Learning

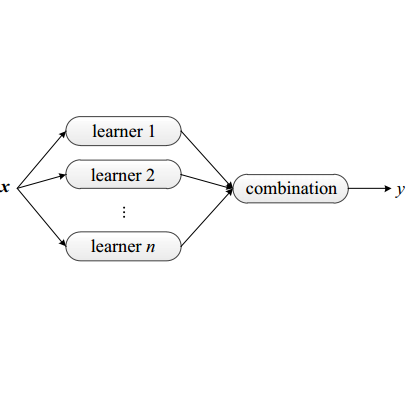
We present a theory of ensemble diversity, explaining the nature of diversity for a wide range of supervised learning scenarios. This challenge, of understanding ensemble diversity, has been referred to as the "holy grail" of ensemble learning, an open research issue for over 30 years. Our framework reveals that diversity is in fact a hidden dimension in the bias-variance decomposition of the ensemble loss. We prove a family of exact bias-variance-diversity decompositions, for both regression and classification, e.g., squared, cross-entropy, and Poisson losses. For losses where an additive bias-variance decomposition is not available (e.g., 0/1 loss) we present an alternative approach, which precisely quantifies the effects of diversity, turning out to be dependent on the label distribution. Experiments show how we can use our framework to understand the diversity-encouraging mechanisms of popular methods: Bagging, Boosting, and Random Forests.