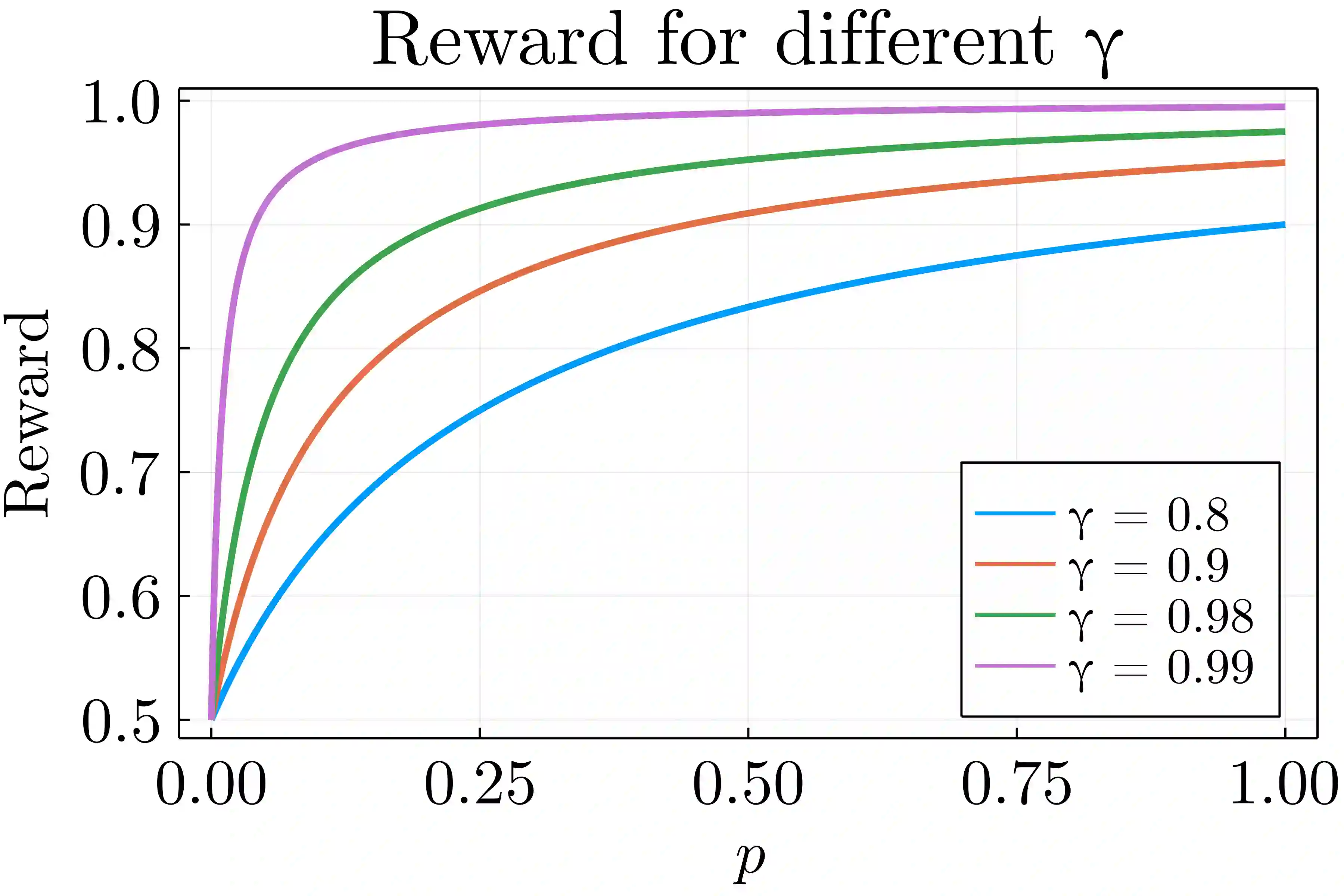
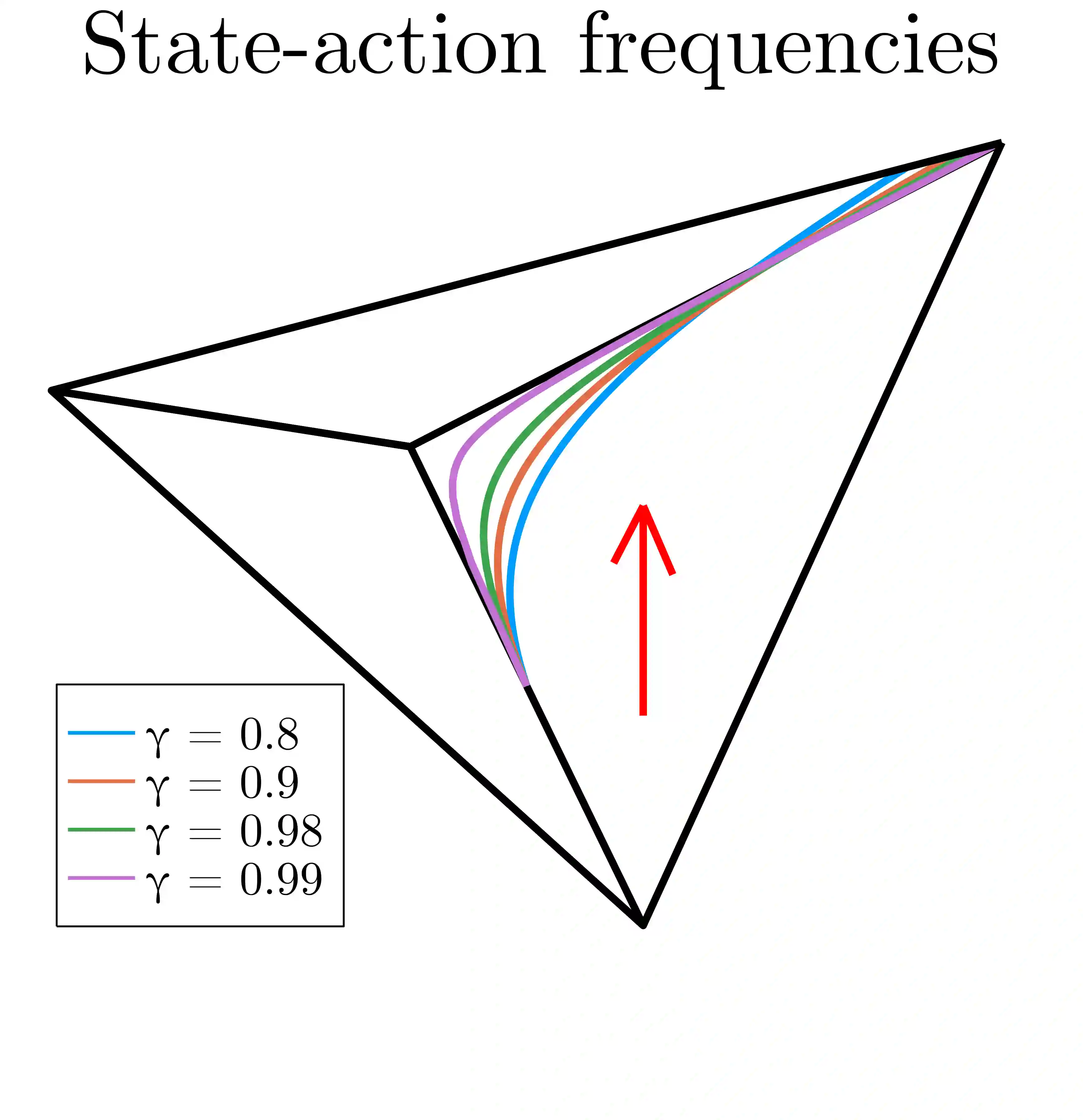
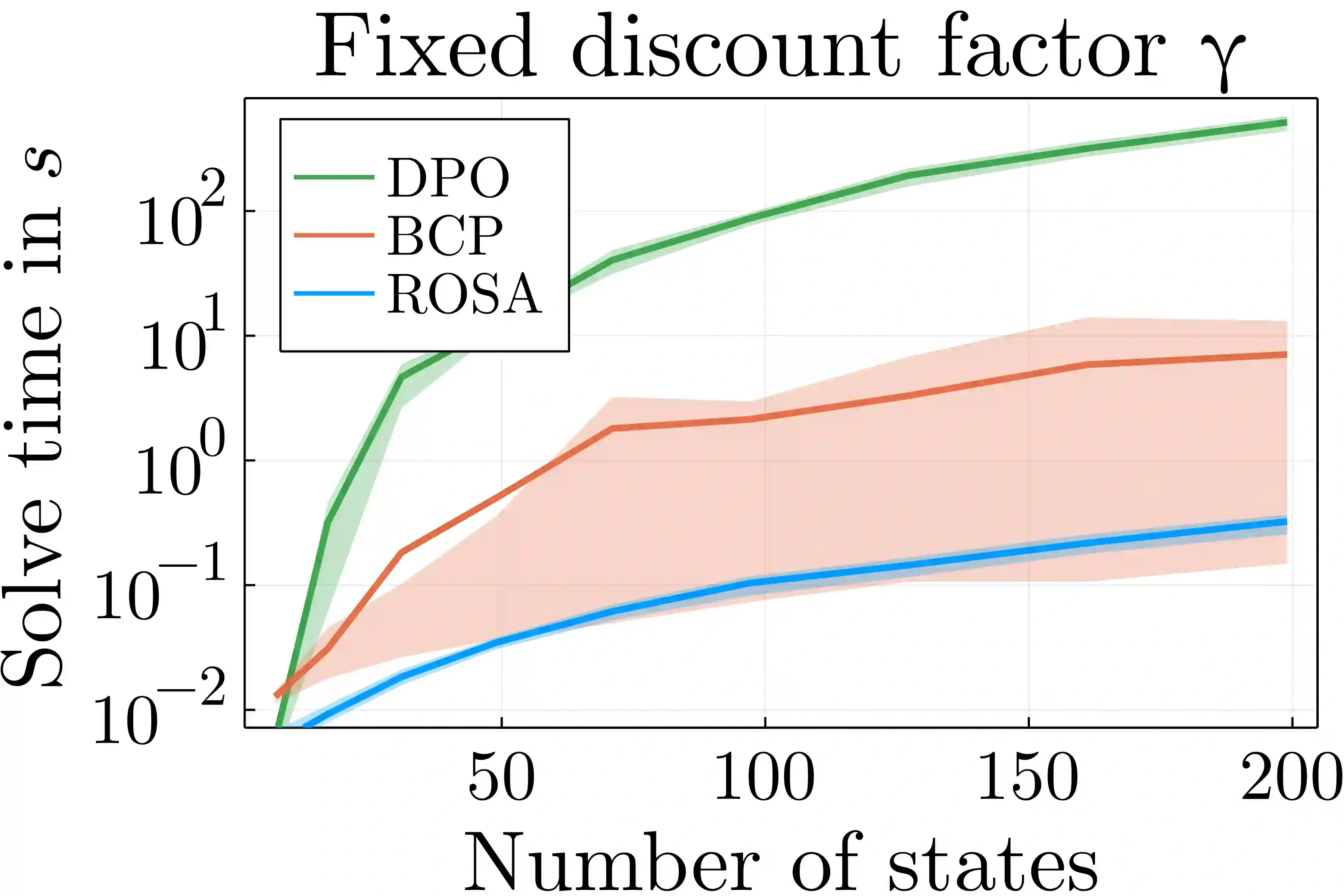
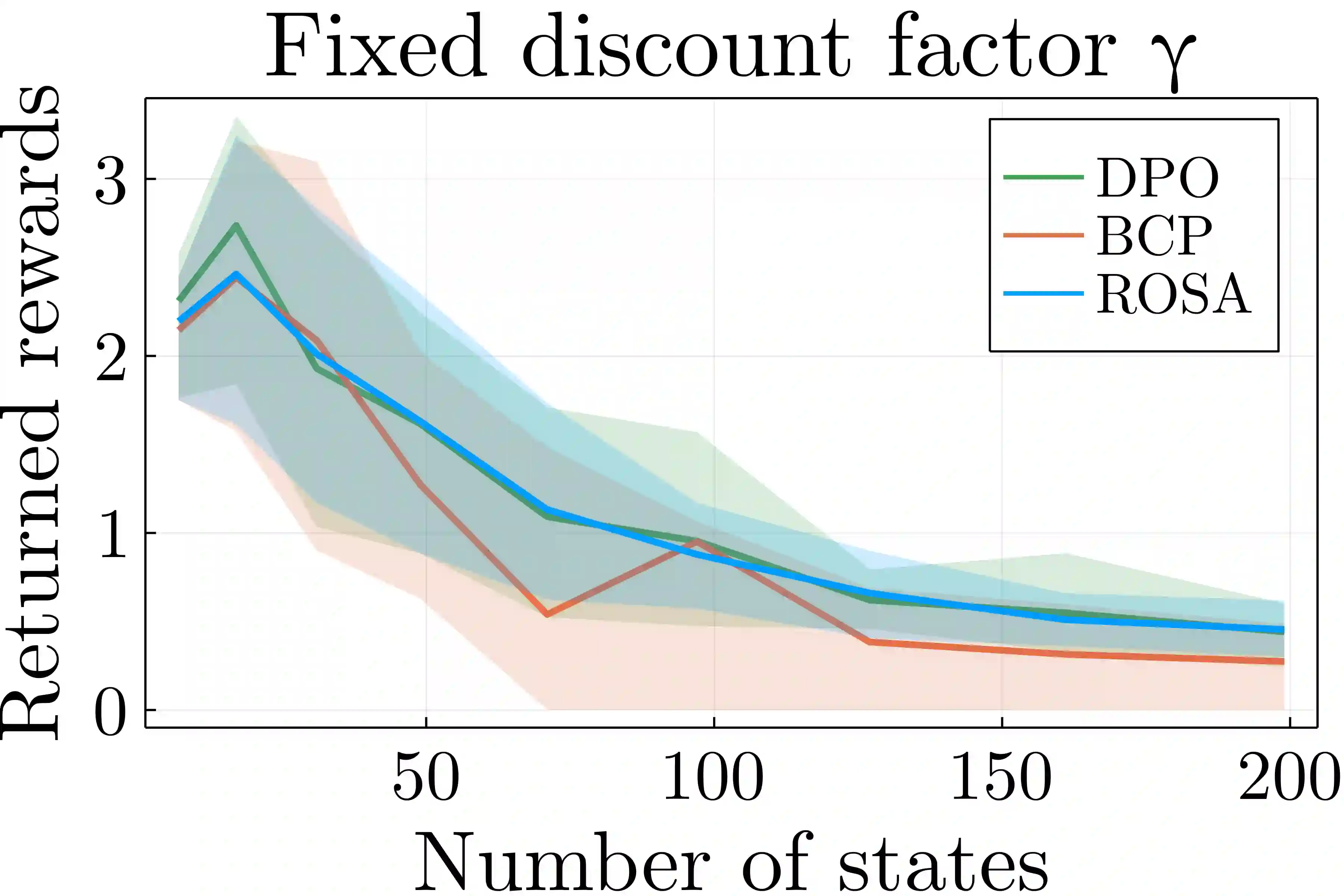
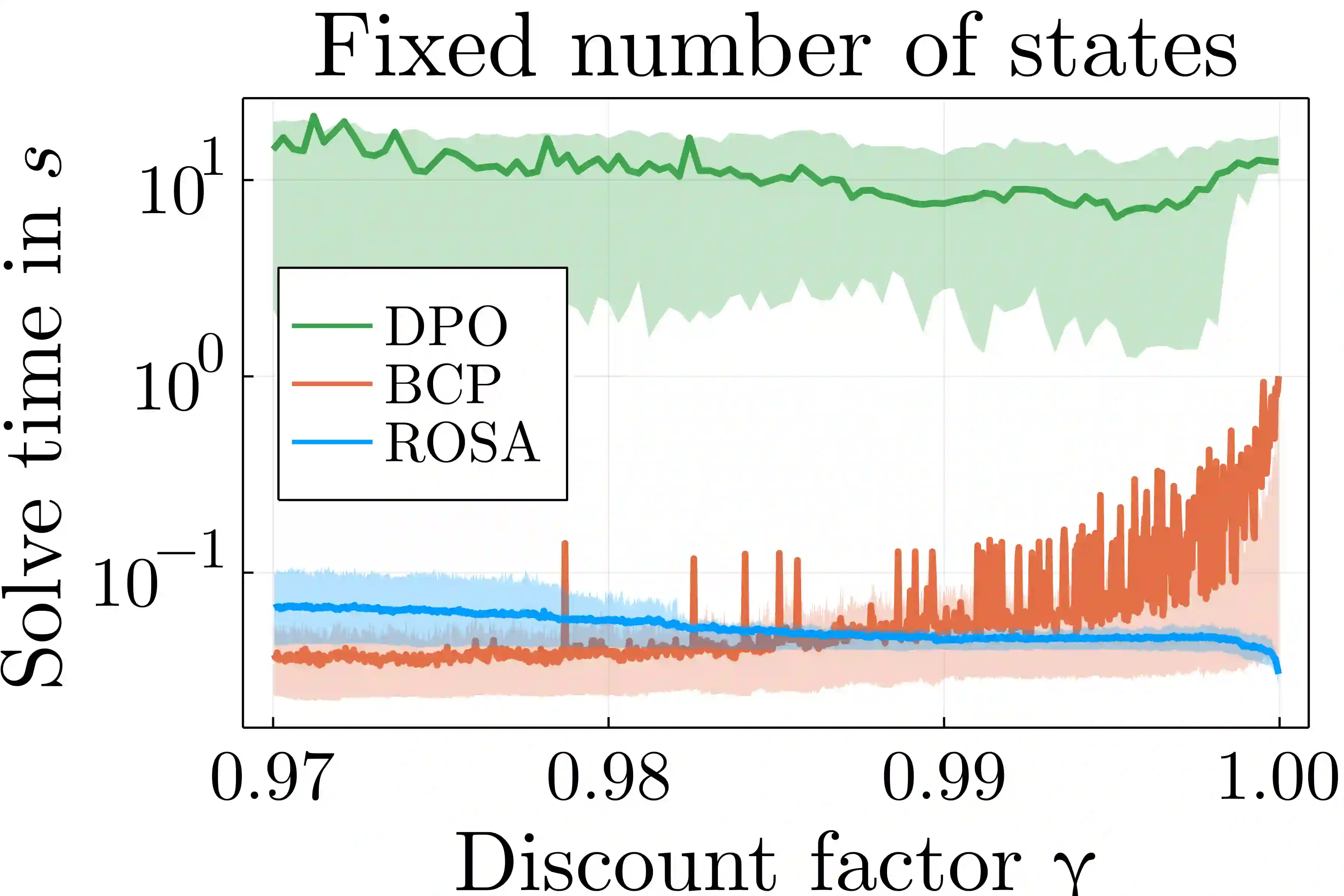
Reward optimization in fully observable Markov decision processes is equivalent to a linear program over the polytope of state-action frequencies. Taking a similar perspective in the case of partially observable Markov decision processes with memoryless stochastic policies, the problem was recently formulated as the optimization of a linear objective subject to polynomial constraints. Based on this we present an approach for Reward Optimization in State-Action space (ROSA). We test this approach experimentally in maze navigation tasks. We find that ROSA is computationally efficient and can yield stability improvements over other existing methods.
翻译:在完全可观测到的Markov决策程序中的奖励优化相当于在州行动频率的多元范围上的一个线性程序。从部分可观测到的Markov决策程序与无内存的随机政策的类似观点来看,这个问题最近被作为线性目标的优化提出来,但受到多种限制。在此基础上,我们提出了一个国家行动空间(ROSA)的奖励优化方法。我们在迷宫导航任务中实验了这一方法。我们发现ROSA在计算上效率很高,并且能够比其他现有方法更稳定。