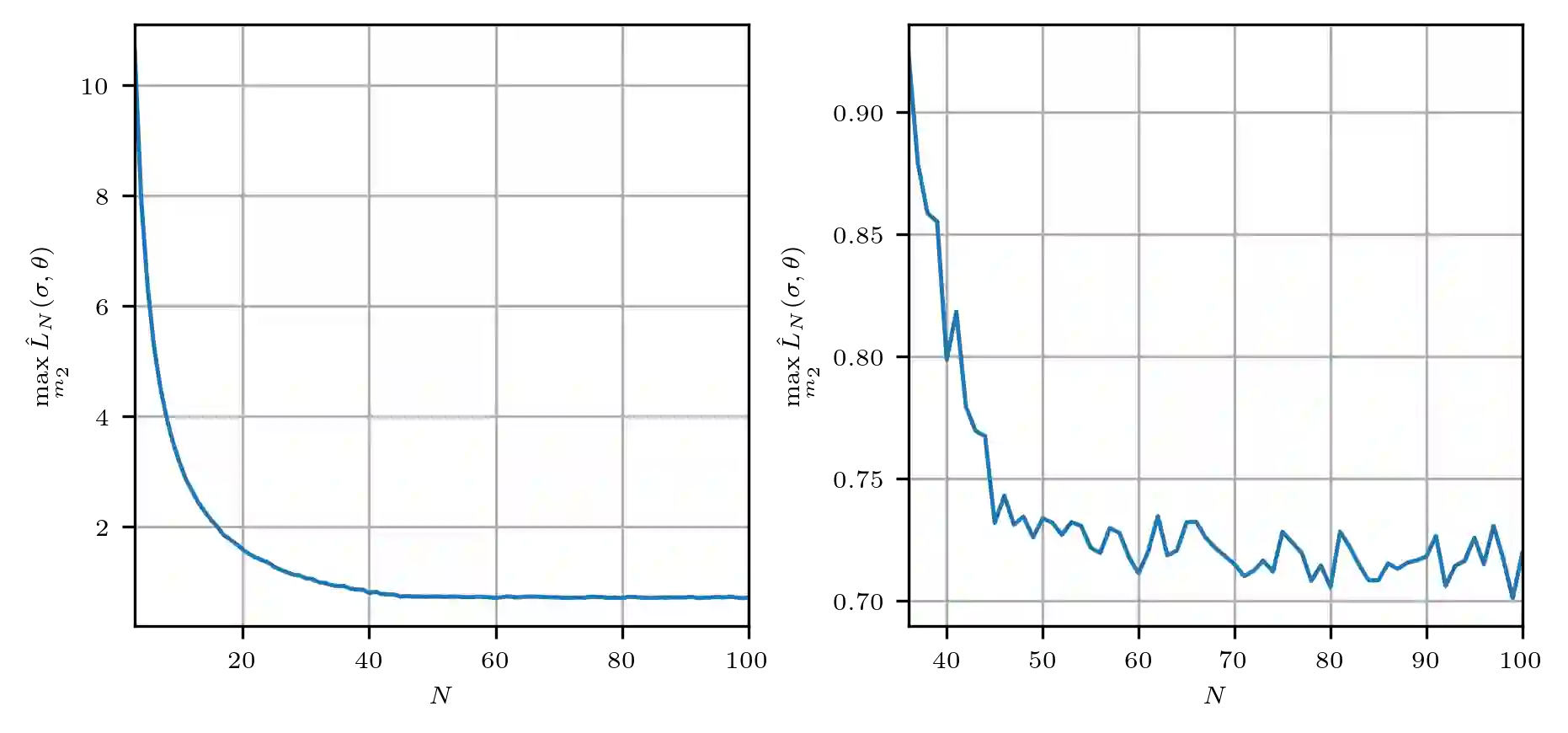
We consider the upper confidence bound strategy for Gaussian multi-armed bandits with known control horizon sizes $N$ and build its limiting description with a system of stochastic differential equations and ordinary differential equations. Rewards for the arms are assumed to have unknown expected values and known variances. A set of Monte-Carlo simulations was performed for the case of close distributions of rewards, when mean rewards differ by the magnitude of order $N^{-1/2}$, as it yields the highest normalized regret, to verify the validity of the obtained description. The minimal size of the control horizon when the normalized regret is not noticeably larger than maximum possible was estimated.
翻译:我们认为,对已知控制地平面大小的高斯族多武装强盗的高度信任约束战略是美元,并采用随机差分方程和普通差分方程来建立其限制性描述,假定武器奖励的预期值和已知差异不明,对报酬分配接近的情况进行了一套蒙特-卡洛模拟,平均奖励因平均数额不同而异,因为平均奖励额通常为1/2美元,以核实所得描述的有效性。