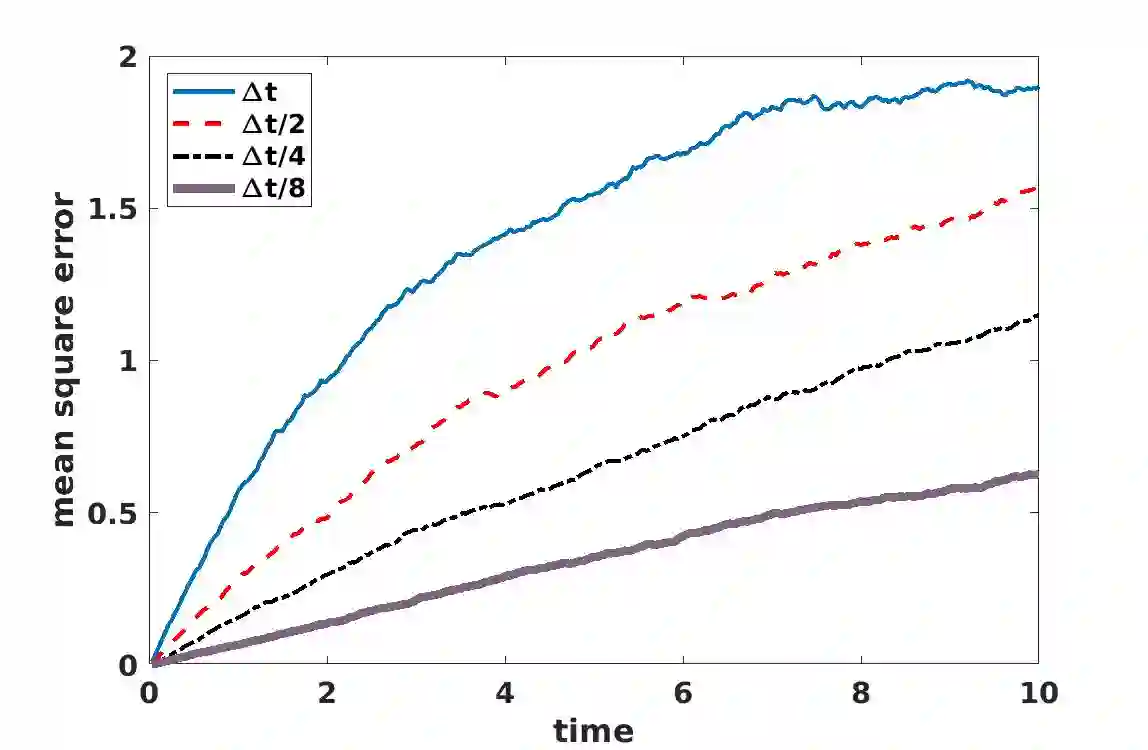
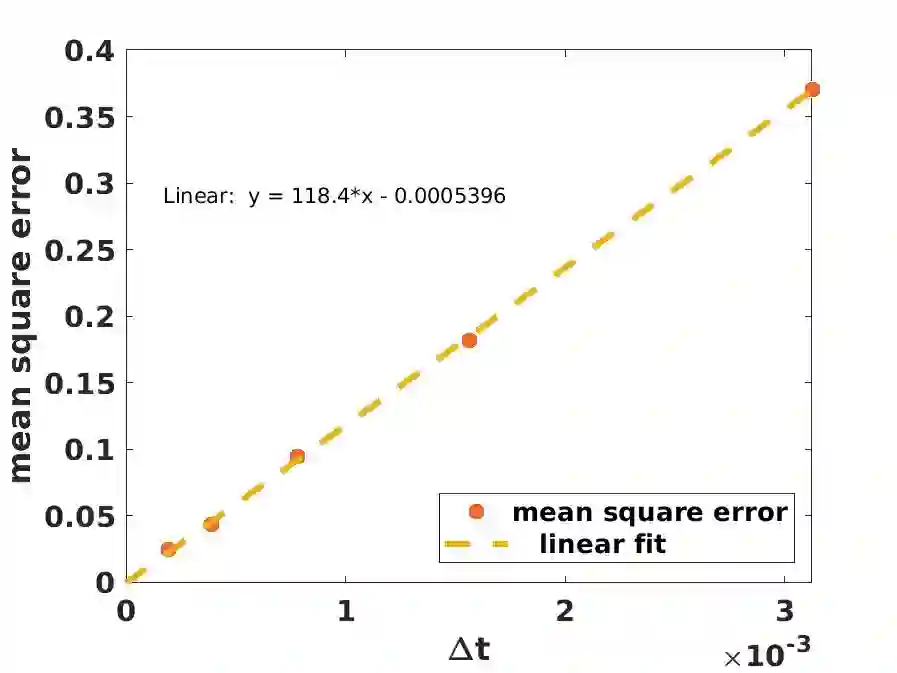
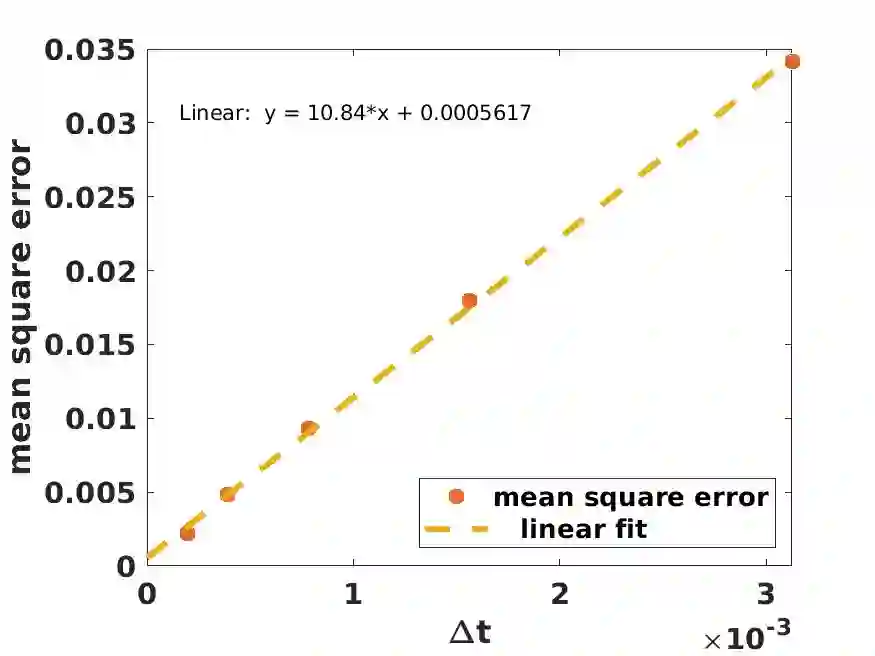
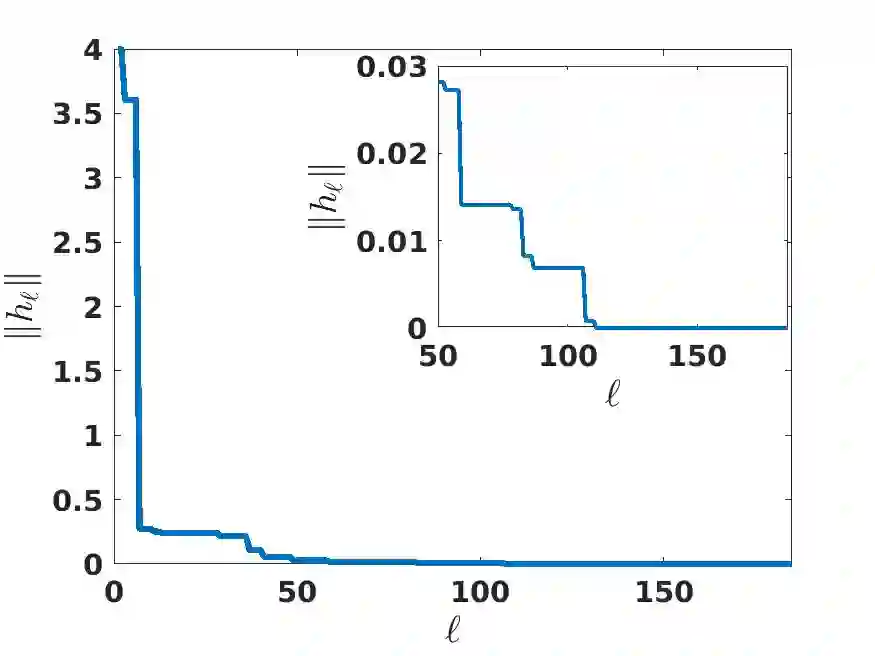
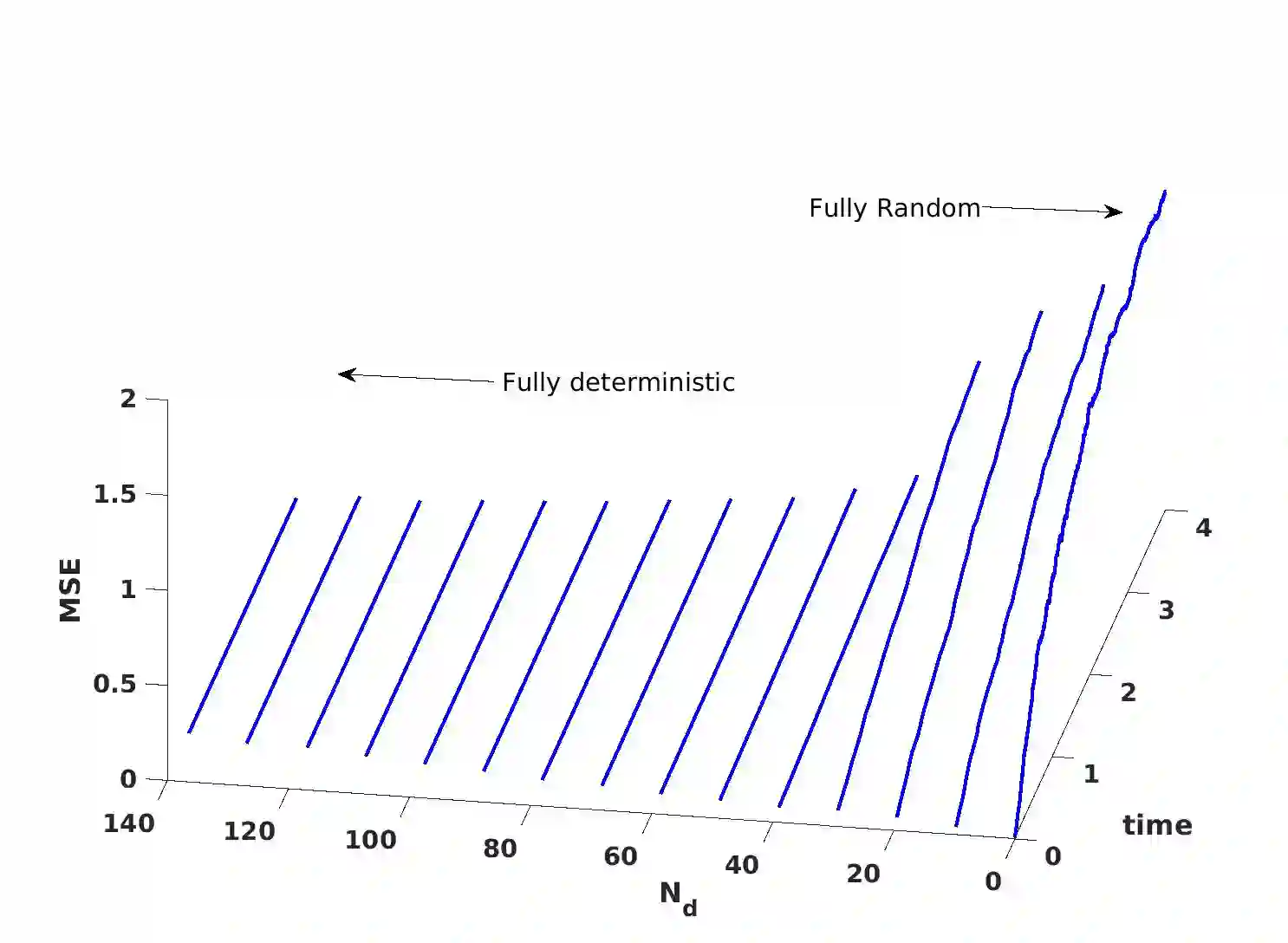
Given the Hamiltonian, the evaluation of unitary operators has been at the heart of many quantum algorithms. Motivated by existing deterministic and random methods, we present a hybrid approach, where Hamiltonians with large amplitude are evaluated at each time step, while the remaining terms are evaluated at random. The bound for the mean square error is obtained, together with a concentration bound. The mean square error consists of a variance term and a bias term, arising respectively from the random sampling of the Hamiltonian terms and the operator splitting error. Leveraging on the bias/variance trade-off, the error can be minimized by balancing the two. The concentration bound provides an estimate on the number of gates. The estimates are verified by using numerical experiments on classical computers.
翻译:鉴于汉密尔顿语,对单一操作员的评价是许多量子算法的核心。受现有确定和随机方法的驱动,我们提出了一个混合方法,即每一步对大振幅的汉密尔顿人进行评价,而其余的术语则随机评价。对平均平方误差进行约束,同时将集中捆绑在一起。中方误差包括因汉密尔顿语术语随机抽样和操作员分裂差错而产生的差异性术语和偏差术语。利用偏差/偏差取法,可以通过平衡两者来尽量减少误差。集中约束提供了门数的估计值。通过在古典计算机上进行数字实验来核实估计数。