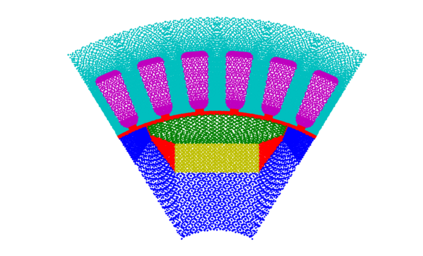
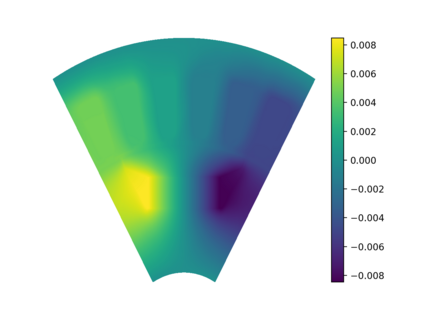
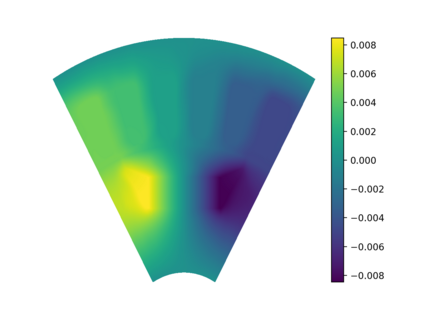
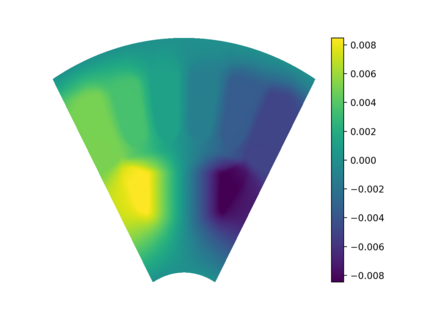
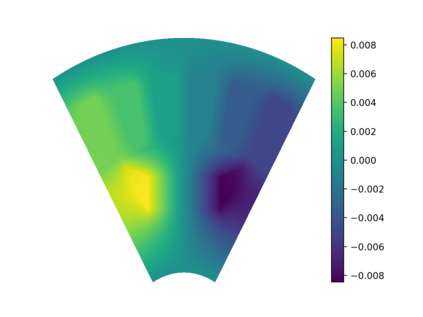
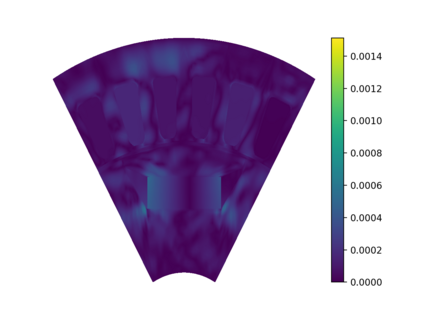
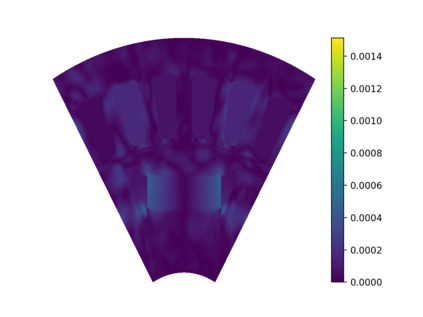
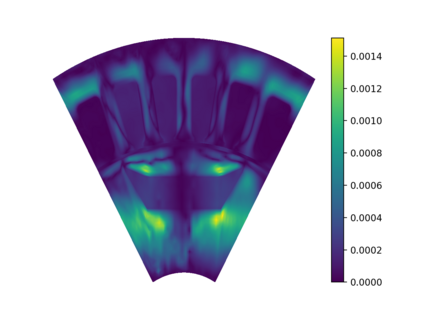
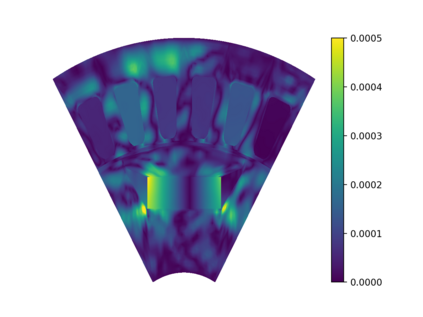
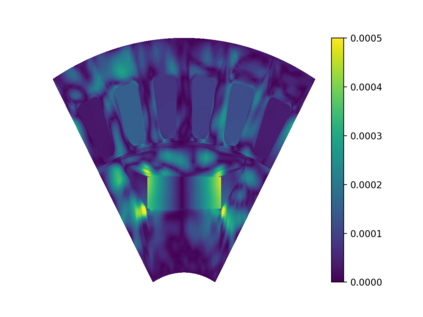
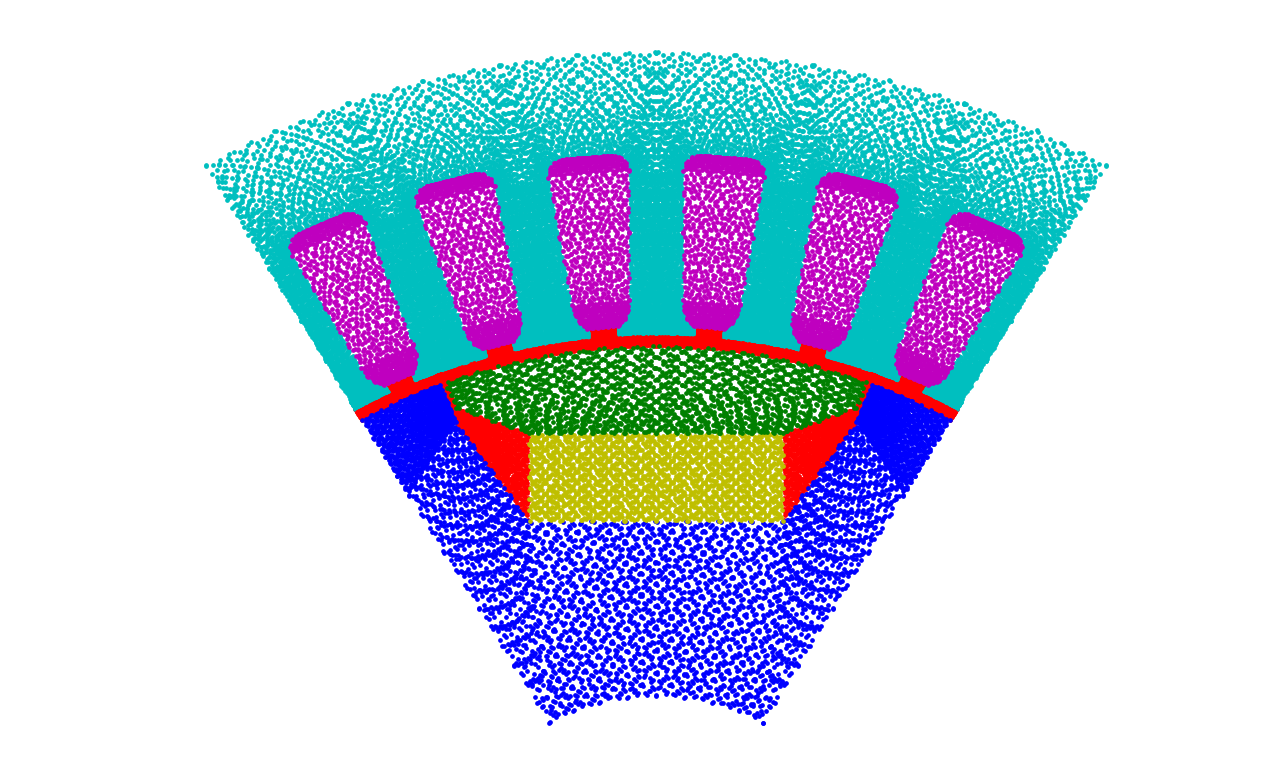
This work presents a deep learning-based framework for the solution of partial differential equations on complex computational domains described with computer-aided design tools. To account for the underlying distribution of the training data caused by spline-based projections from the reference to the physical domain, a variational neural solver equipped with an importance sampling scheme is developed, such that the loss function based on the discretized energy functional obtained after the weak formulation is modified according to the sample distribution. To tackle multi-patch domains possibly leading to solution discontinuities, the variational neural solver is additionally combined with a domain decomposition approach based on the Discontinuous Galerkin formulation. The proposed neural solver is verified on a toy problem and then applied to a real-world engineering test case, namely that of electric machine simulation. The numerical results show clearly that the neural solver produces physics-conforming solutions of significantly improved accuracy.
翻译:这项工作为解决与计算机辅助设计工具相描述的复杂计算域的局部差异方程式提供了一个深层次的学习框架。为了说明从物理域参考中根据基于样条的预测得出的培训数据的基本分布情况,开发了一个配有重要取样计划的变异神经求解器,以便根据微弱配方根据样本分布修改后获得的离散能源功能而产生的损失功能。为了处理可能导致溶解中断的多批域,变异神经求解器与基于不连续的加列金配方法的域分解法相配合。拟议的神经求解器根据一个小问题进行核查,然后应用于一个真实世界工程试验案例,即电机模拟。数字结果清楚地表明,神经求解器产生精确性显著提高的物理兼容性解决方案。