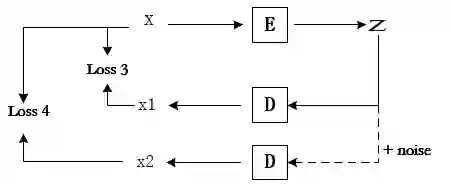
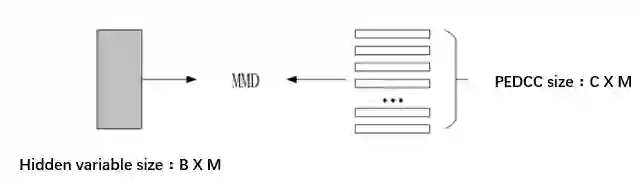
In this paper, we propose an end-to-end image clustering auto-encoder algorithm: ICAE. The algorithm uses PEDCC (Predefined Evenly-Distributed Class Centroids) as the clustering centers of the images, which ensures the inter-class distance of latent features is maximal, and adds data distribution constraint, data augmentation constraint, auto-encoder reconstruction loss constraint and latent features plus noise constraint to improve clustering performance. Specifically, we perform one-to-one data augmentation such as rotation, shear, and shift before data is input to the encoder to learn the more effective features. The data and the enhanced data are simultaneously input into the auto-encoder to obtain latent features and augmented latent features whose similarity are constrained by an augmentation loss. Then, making use of the MMD distance, we combine the latent features and augmented latent features to make their distribution close to the PEDCC distribution (uniform distribution between classes, Dirac distribution within the class) to further learn the features used for clustering. At the same time, the MSE of the original input image and reconstructed image is used as reconstruction constraint, and the noise is added to the latent features to build generalization constraint to improve the generalization ability. Finally, extensive experiments on three common datasets MNIST, Fashion-MNIST, COIL20 are conducted. The experimental results show that the algorithm has achieved the best clustering results so far, and also has good generalization ability. In addition, we can use the pre-defined PEDCC class centers, and the decoding module of the auto-encoder to clearly generate the samples of each class. The code can be downloaded at xxx!
翻译:在本文中, 我们提出一个自动编码器的终端到终端图像聚合自动编码算法 : ICAE 。 算法使用 PEDCC( 预定义的均分类中枢) 作为图像的集成中心, 以确保潜质功能的跨级距离为最大值, 并增加数据分配限制、 数据增强限制、 自动编码重建损失限制和潜在特性, 加上噪音限制, 以提高组合性能。 具体地说, 我们执行一对一的数据增强, 如旋转、 剪切, 和在数据转换之前, 将数据输入到编码器中, 学习更有效的特性。 数据和增强的数据同时输入到自动编码中, 以获得潜值特性, 增强潜在特性, 并增加潜在特性, 使用MDMAC 最小值距离, 将潜在特性合并, 使其接近 PEDCC 分布( 类之间的单级分布, Dirac 分布在类中) 以进一步学习集成的特性。 同时, 原始输入图像和图像重建的MDR 的模型中继 能力 将被明确用于 重建的模型 。 最后, 将生成的机能提升到普通的模型的模型 。 升级 将 进行 进行 进行 进行 进行 。 将 进行 进行 进行 进行 进行 进行 的 进行 进行 进行 进行 进行 进行 进行 常规 的 的 的 进行 进行 的 的 的 的 进行 进行 的 的 进行 进行 的 进行 的 的 的 进行 的 和 进行 的 的 的 进行 的 进行 进行 进行 进行 进行 进行 进行 进行 进行 进行 进行 进行 进行 进行 的 的 进行 进行 的 进行 的 进行 的 的 进行 进行 进行 进行 进行 进行 进行 进行 进行 的 进行 进行 进行 进行 进行 的 进行 进行 进行 进行 的 的 的 进行 的 的 进行 进行 进行 进行 进行 进行 进行 进行 进行 进行 进行 进行 进行 的 的 的 进行