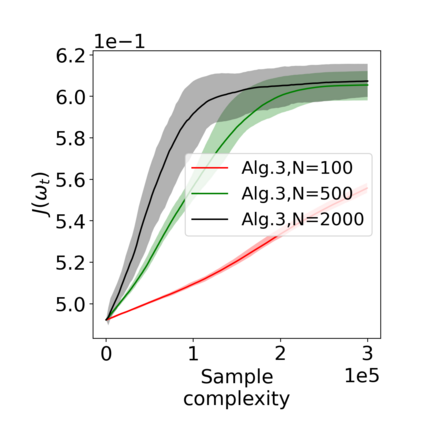
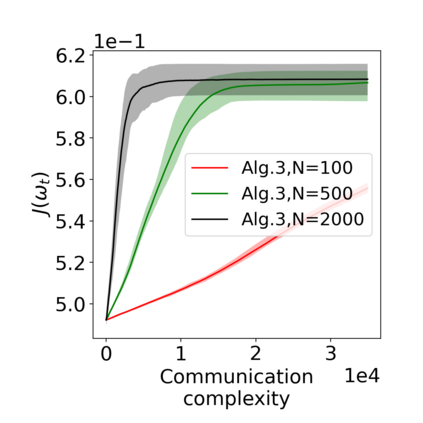
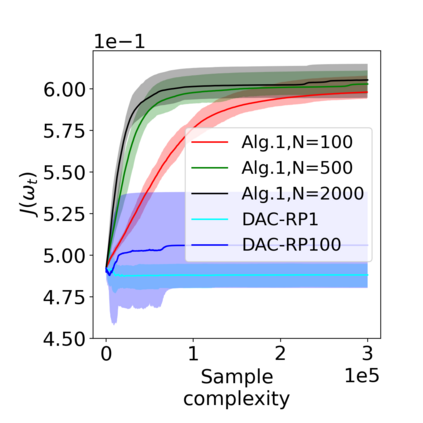
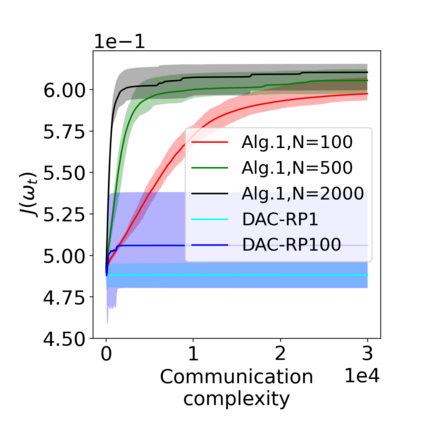
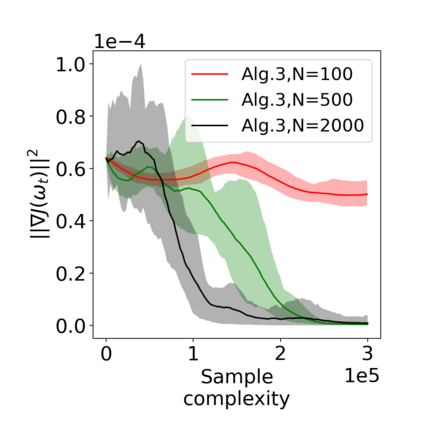
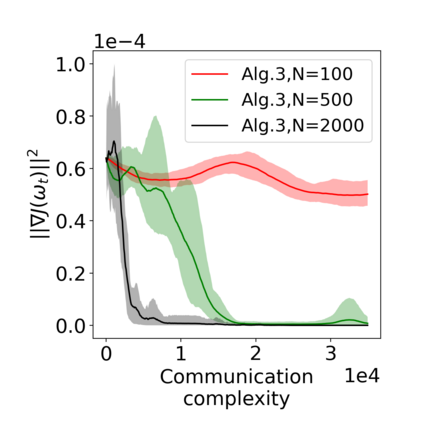
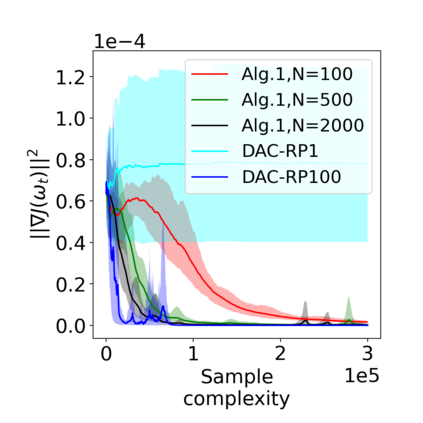
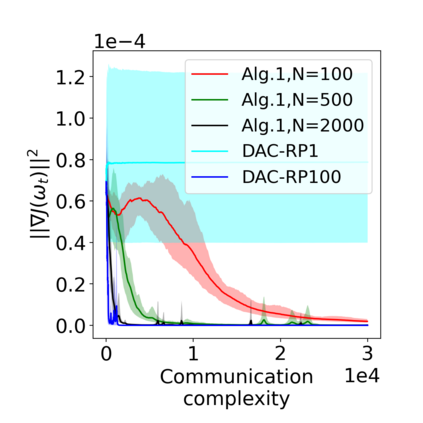
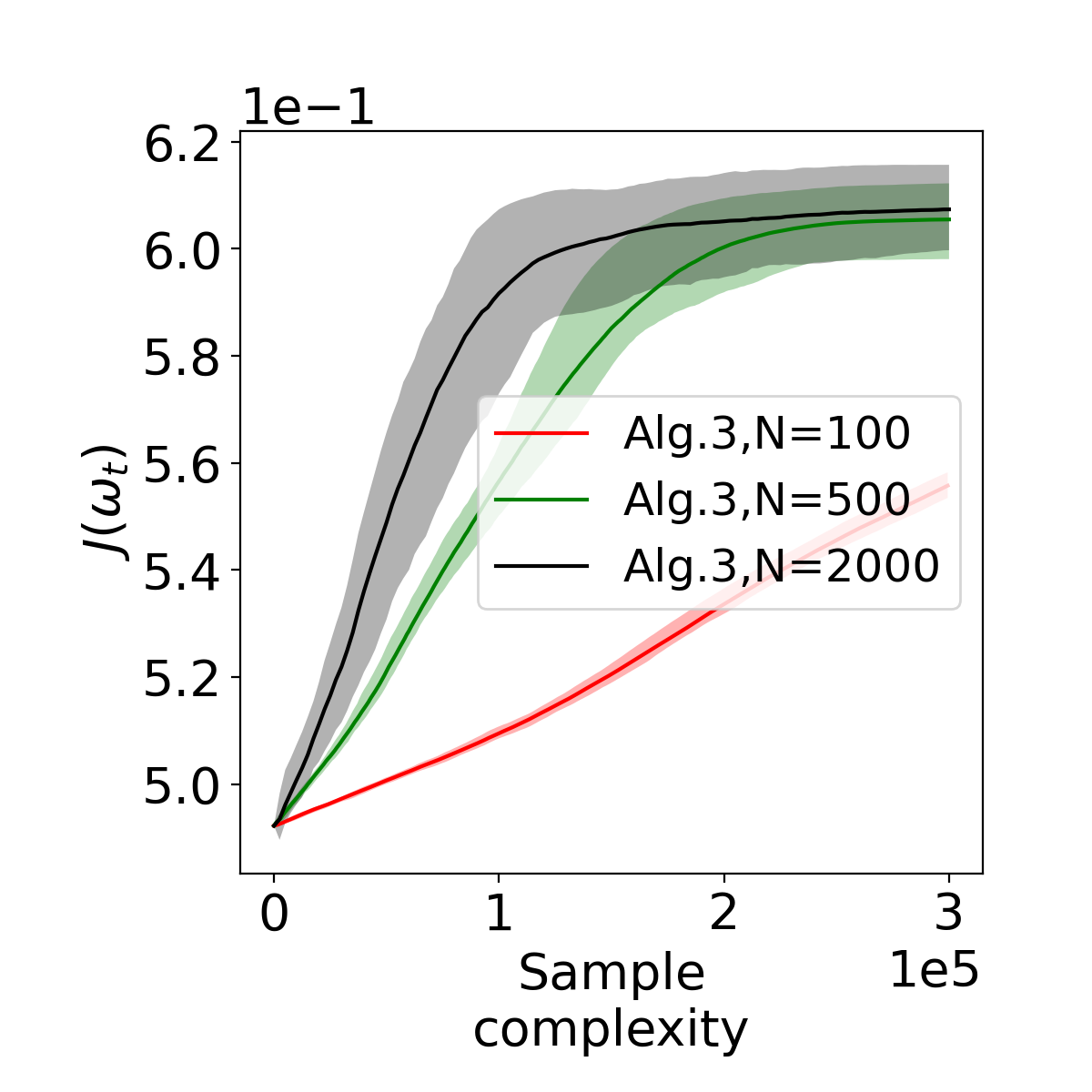
Actor-critic (AC) algorithms have been widely adopted in decentralized multi-agent systems to learn the optimal joint control policy. However, existing decentralized AC algorithms either do not preserve the privacy of agents or are not sample and communication-efficient. In this work, we develop two decentralized AC and natural AC (NAC) algorithms that are private, and sample and communication-efficient. In both algorithms, agents share noisy information to preserve privacy and adopt mini-batch updates to improve sample and communication efficiency. Particularly for decentralized NAC, we develop a decentralized Markovian SGD algorithm with an adaptive mini-batch size to efficiently compute the natural policy gradient. Under Markovian sampling and linear function approximation, we prove the proposed decentralized AC and NAC algorithms achieve the state-of-the-art sample complexities $\mathcal{O}\big(\epsilon^{-2}\ln(\epsilon^{-1})\big)$ and $\mathcal{O}\big(\epsilon^{-3}\ln(\epsilon^{-1})\big)$, respectively, and the same small communication complexity $\mathcal{O}\big(\epsilon^{-1}\ln(\epsilon^{-1})\big)$. Numerical experiments demonstrate that the proposed algorithms achieve lower sample and communication complexities than the existing decentralized AC algorithm.
翻译:在分散的多试剂系统中广泛采用Acor-critic(AC)算法,以学习最佳的联合控制政策。然而,现有的分散的AC算法要么不保护代理人的隐私,要么没有抽样和通信效率。在这项工作中,我们开发了两种分散的AC和自然AC(NAC)算法,它们是私人的,以及抽样和通信效率。在这两种算法中,代理共享噪音信息以维护隐私,并采用小型批量更新以提高抽样和通信效率。特别是在分散的NAC中,我们开发了一种分散的Markovian SGD算法,具有适应性微型批量大小,以高效地计算自然政策梯度。在Markovian抽样和线性功能接近下,我们证明拟议的分散的AC和自然AC(NAC)算法实现了最先进的样本复杂性$\macal{O ⁇ big(\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\