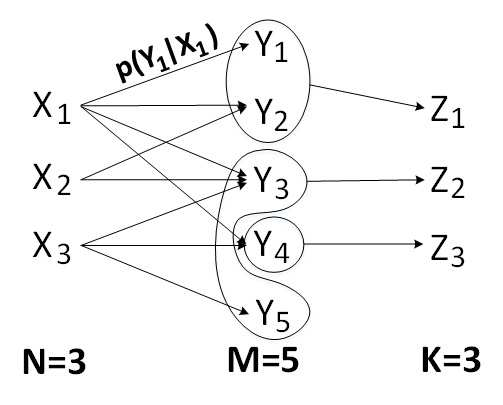
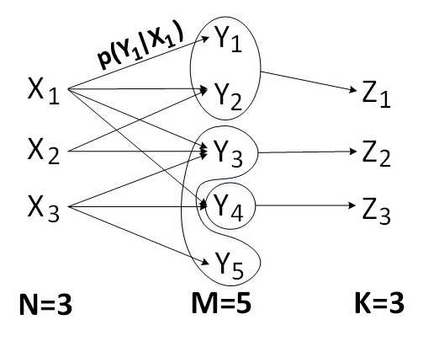
Partitioning algorithms play a key role in many scientific and engineering disciplines. A partitioning algorithm divides a set into a number of disjoint subsets or partitions. Often, the quality of the resulted partitions is measured by the amount of impurity in each partition, the smaller impurity the higher quality of the partitions. In general, for a given impurity measure specified by a function of the partitions, finding the minimum impurity partitions is an NP-hard problem. Let $M$ be the number of $N$-dimensional elements in a set and $K$ be the number of desired partitions, then an exhaustive search over all the possible partitions to find a minimum partition has the complexity of $O(K^M)$ which quickly becomes impractical for many applications with modest values of $K$ and $M$. Thus, many approximate algorithms with polynomial time complexity have been proposed, but few provide bounded guarantee. In this paper, an upper bound and a lower bound for a class of impurity functions are constructed. Based on these bounds, we propose a low-complexity partitioning algorithm with bounded guarantee based on the maximum likelihood principle. The theoretical analyses on the bounded guarantee of the algorithms are given for two well-known impurity functions Gini index and entropy. When $K \geq N$, the proposed algorithm achieves state-of-the-art results in terms of lowest approximations and polynomial time complexity $O(NM)$. In addition, a heuristic greedy-merge algorithm having the time complexity of $O((N-K)N^2+NM)$ is proposed for $K<N$. Although the greedy-merge algorithm does not provide a bounded guarantee, its performance is comparable to that of the state-of-the-art methods. Our results also generalize some well-known information-theoretic bounds such as Fano's inequality and Boyd-Chiang's bound.
翻译:分割算法在许多科学和工程学科中发挥着关键作用 。 分割算法将一组内脏元素分为若干脱节子集或分区 。 通常, 结果分割法的质量以每个分区的杂质量、 小杂质和分区质量较高来衡量 。 一般来说, 对于由分区函数指定的某种杂质度测量, 发现最小杂质分区是一个NP- 硬性的问题 。 让美元作为一组内脏元素的数量, 美元作为想要的分区数量, 然后对所有可能的复杂度进行彻底的搜索以找到最小的分区 $( KNM ) 。 而对于每个分区的杂质量, 最小的杂质质量是更低的 。 因此, 提出了许多具有多元性时间复杂性的近似算法, 但很少提供约束性的保证 。 在本文中, 一个用于某类杂质添加的内脏功能的上限和下限值的内值值值值值值。 基于这些界限, 我们建议对最低的内脏的内脏运算法结果进行一个最有可能的内基价值分析 。