An Online Efficient Two-Scale Reduced Basis Approach for the Localized Orthogonal Decomposition

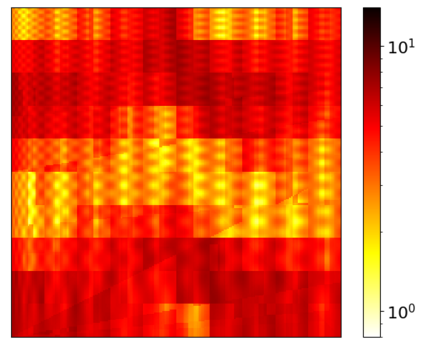
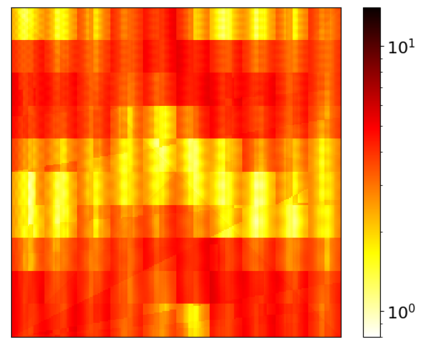
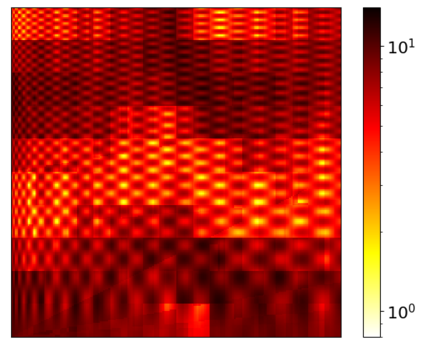
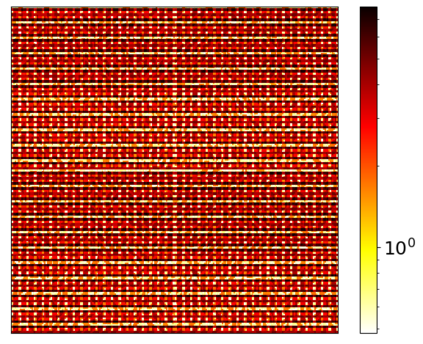
We are concerned with employing Model Order Reduction (MOR) to efficiently solve parameterized multiscale problems using the Localized Orthogonal Decomposition (LOD) multiscale method. Like many multiscale methods, the LOD follows the idea of separating the problem into localized fine-scale subproblems and an effective coarse-scale system derived from the solutions of the local problems. While the Reduced Basis (RB) method has already been used to speed up the solution of the fine-scale problems, the resulting coarse system remained untouched, thus limiting the achievable speed up. In this work we address this issue by applying the RB methodology to a new two-scale formulation of the LOD. By reducing the entire two-scale system, this two-scale Reduced Basis LOD (TSRBLOD) approach, yields reduced order models that are completely independent from the size of the coarse mesh of the multiscale approach, allowing an efficient approximation of the solutions of parameterized multiscale problems even for very large domains. A rigorous and efficient a posteriori estimator bounds the model reduction error, taking into account the approximation error for both the local fine-scale problems and the global coarse-scale system.