A computational macroscale model for the time fractional poroelasticity problem in fractured and heterogeneous media

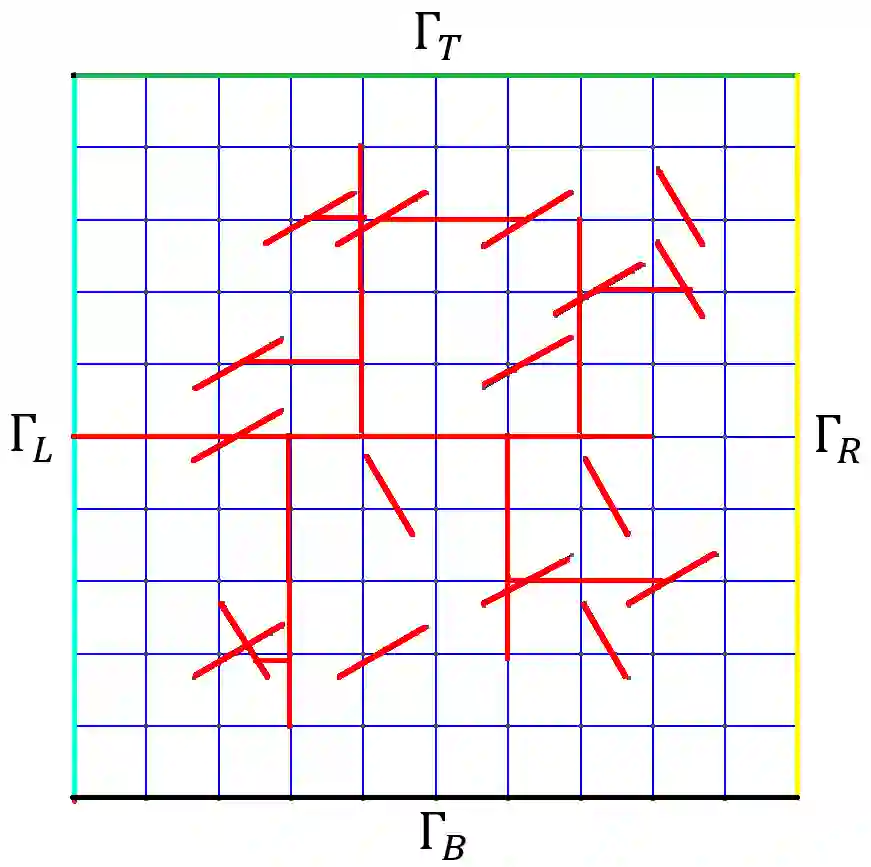
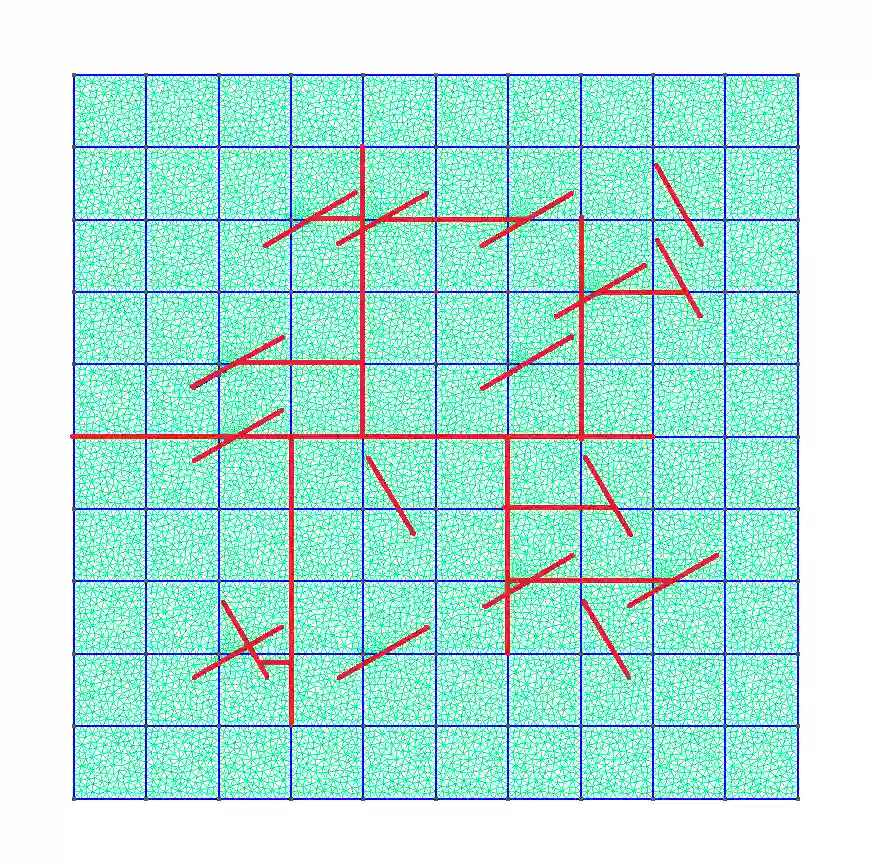
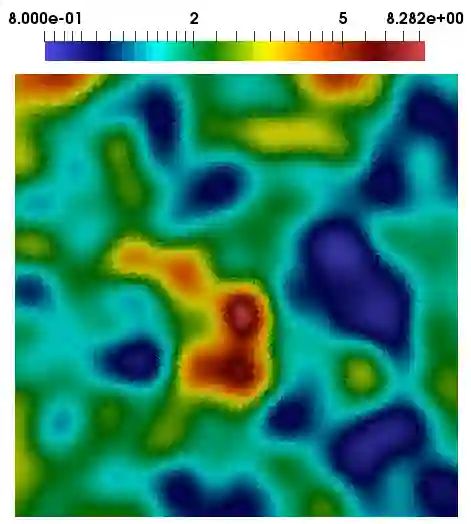
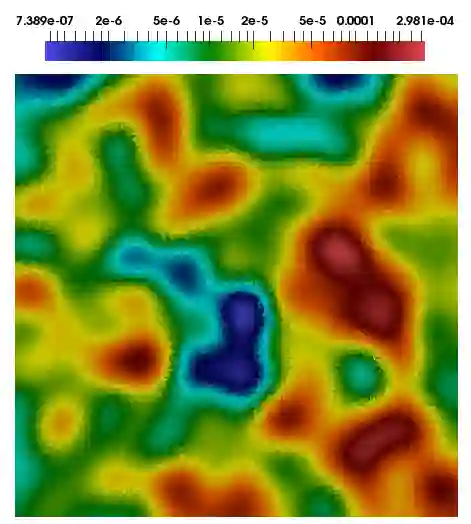
In this work, we introduce a time memory formalism in poroelasticity model that couples the pressure and displacement. We assume this multiphysics process occurs in multicontinuum media. The mathematical model contains a coupled system of equations for pressures in each continuum and elasticity equations for displacements of the medium. We assume that the temporal dynamics is governed by fractional derivatives following some works in the literature. We derive an implicit finite difference approximation for time discretization based on the Caputo time fractional derivative. A Discrete Fracture Model (DFM) is used to model fluid flow through fractures and treat the complex network of fractures. We assume different fractional powers in fractures and matrix due to slow and fast dynamics. We develop a coarse grid approximation based on the Generalized Multiscale Finite Element Method (GMsFEM), where we solve local spectral problems for construction of the multiscale basis functions. We present numerical results for the two-dimensional model problems in fractured heterogeneous porous media. We investigate error analysis between reference (fine-scale) solution and multiscale solution with different numbers of multiscale basis functions. The results show that the proposed method can provide good accuracy on a coarse grid.