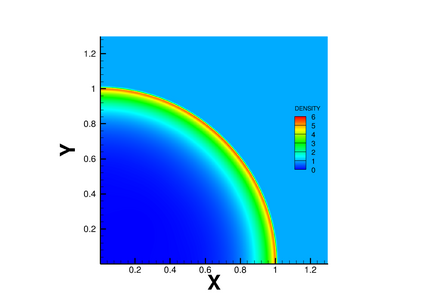
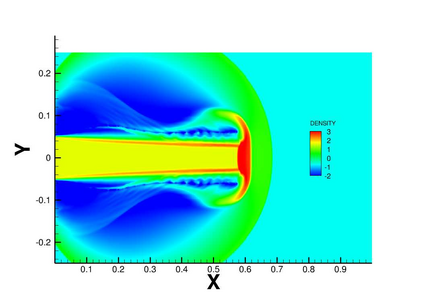
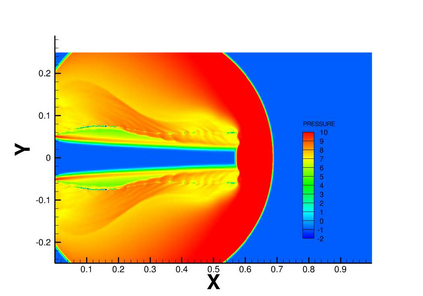
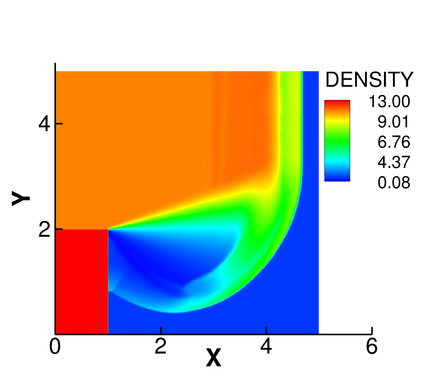
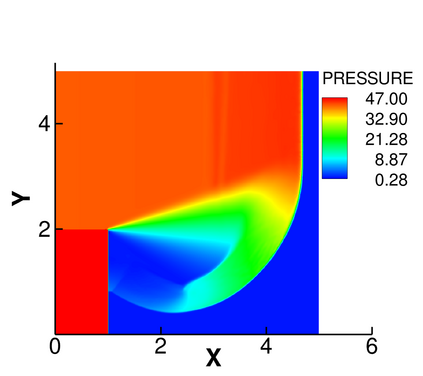
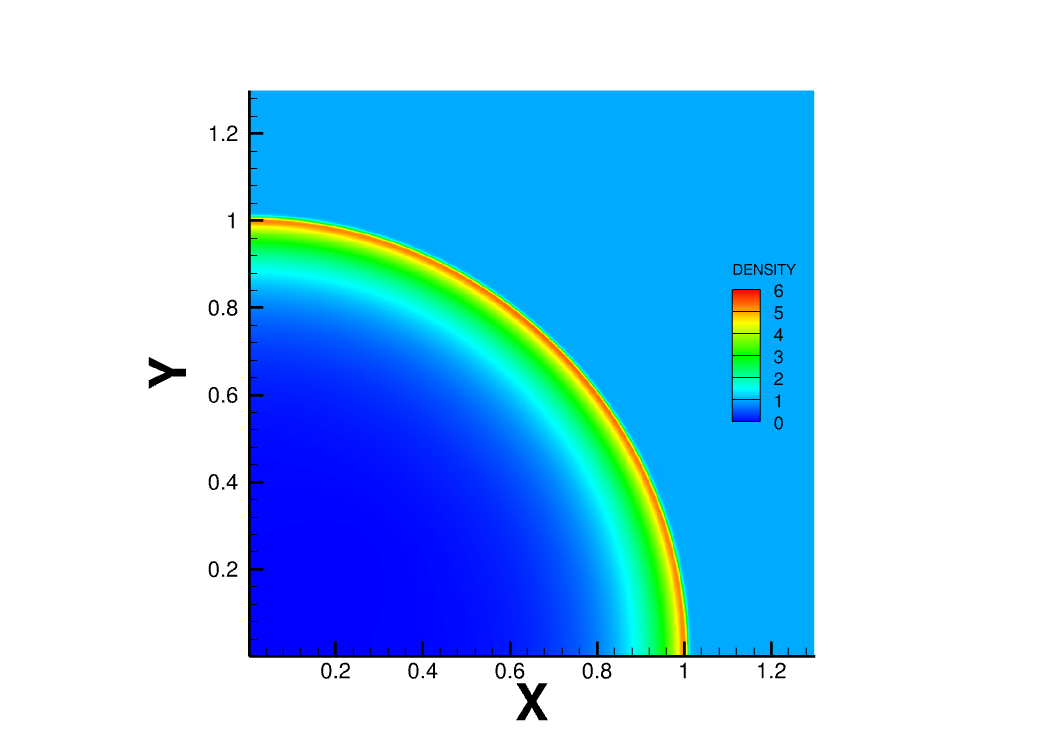
We develop a simple, high-order, conservative and robust positivity-preserving sweeping procedure for the density and the nonlinear pressure function in the compressible Euler equations. Using the scaling limiter in Zhang and Shu (2010), we obtain a nontrivial extension of the scalar sweeping technique in Liu, Cheng, and Shu (2016) for the positivity of pressure. The sweeping procedure developed in this paper is a post-processing technique, which can be applied to any concave functions of the conserved variables in hyperbolic conservation law systems. Thus, it has applications beyond the Euler equations. This procedure preserves positivity and conservation of physical quantities without destroying the accuracy of the underlying scheme. The algorithm works for general schemes including finite difference, finite-volume and discontinuous Galerkin methods; however, in this paper we focus on finite-difference weighted essentially non-oscillatory (WENO) methods. We provide numerical tests of the fifth order finite difference WENO scheme to demonstrate the accuracy and robustness of the technique.
翻译:暂无翻译