Occupancy Information Ratio: Infinite-Horizon, Information-Directed, Parameterized Policy Search

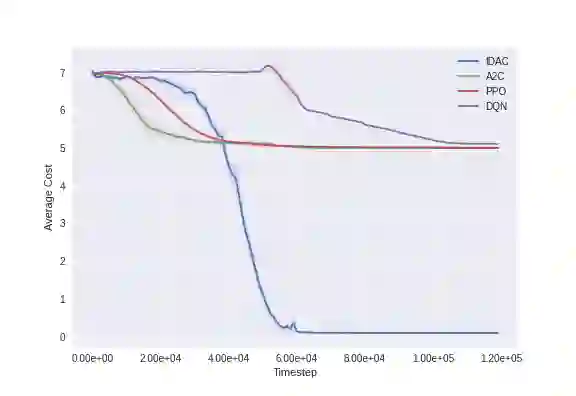
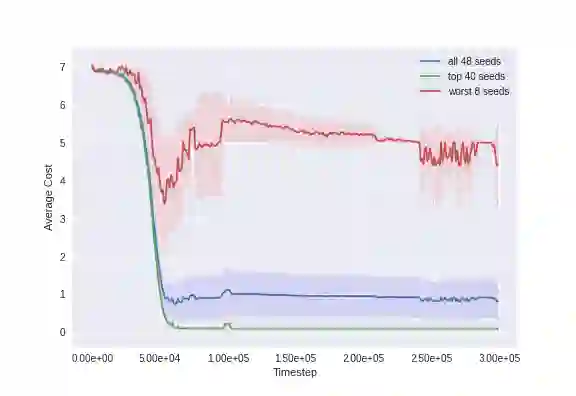
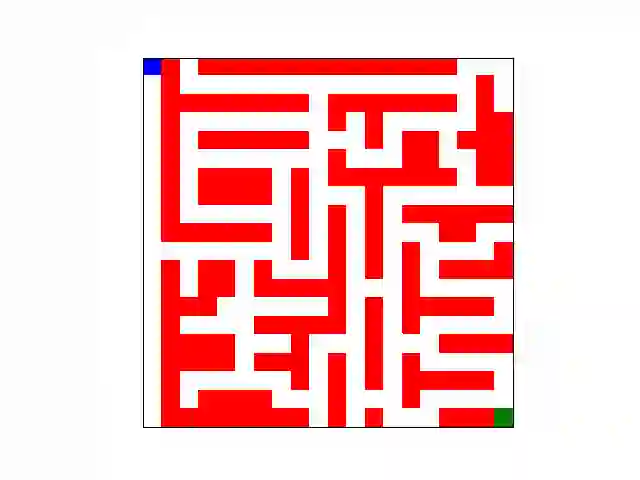
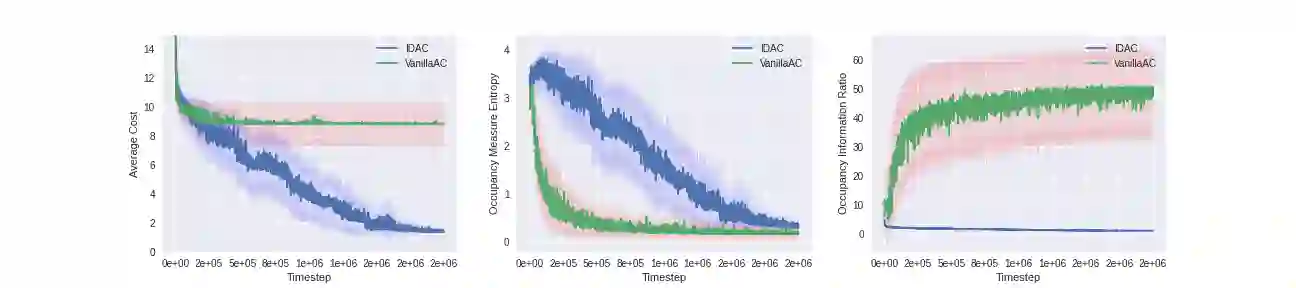
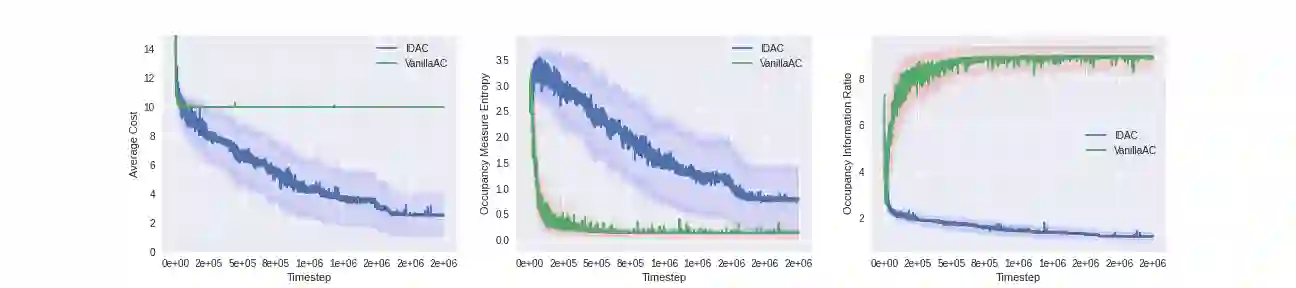
We develop a new measure of the exploration/exploitation trade-off in infinite-horizon reinforcement learning problems called the occupancy information ratio (OIR), which is comprised of a ratio between the infinite-horizon average cost of a policy and the entropy of its long-term state occupancy measure. The OIR ensures that no matter how many trajectories an RL agent traverses or how well it learns to minimize cost, it maintains a healthy skepticism about its environment, in that it defines an optimal policy which induces a high-entropy occupancy measure. Different from earlier information ratio notions, OIR is amenable to direct policy search over parameterized families, and exhibits hidden quasiconcavity through invocation of the perspective transformation. This feature ensures that under appropriate policy parameterizations, the OIR optimization problem has no spurious stationary points, despite the overall problem's nonconvexity. We develop for the first time policy gradient and actor-critic algorithms for OIR optimization based upon a new entropy gradient theorem, and establish both asymptotic and non-asymptotic convergence results with global optimality guarantees. In experiments, these methodologies outperform several deep RL baselines in problems with sparse rewards, where many trajectories may be uninformative and skepticism about the environment is crucial to success.