Benign Overfitting in Time Series Linear Model with Over-Parameterization

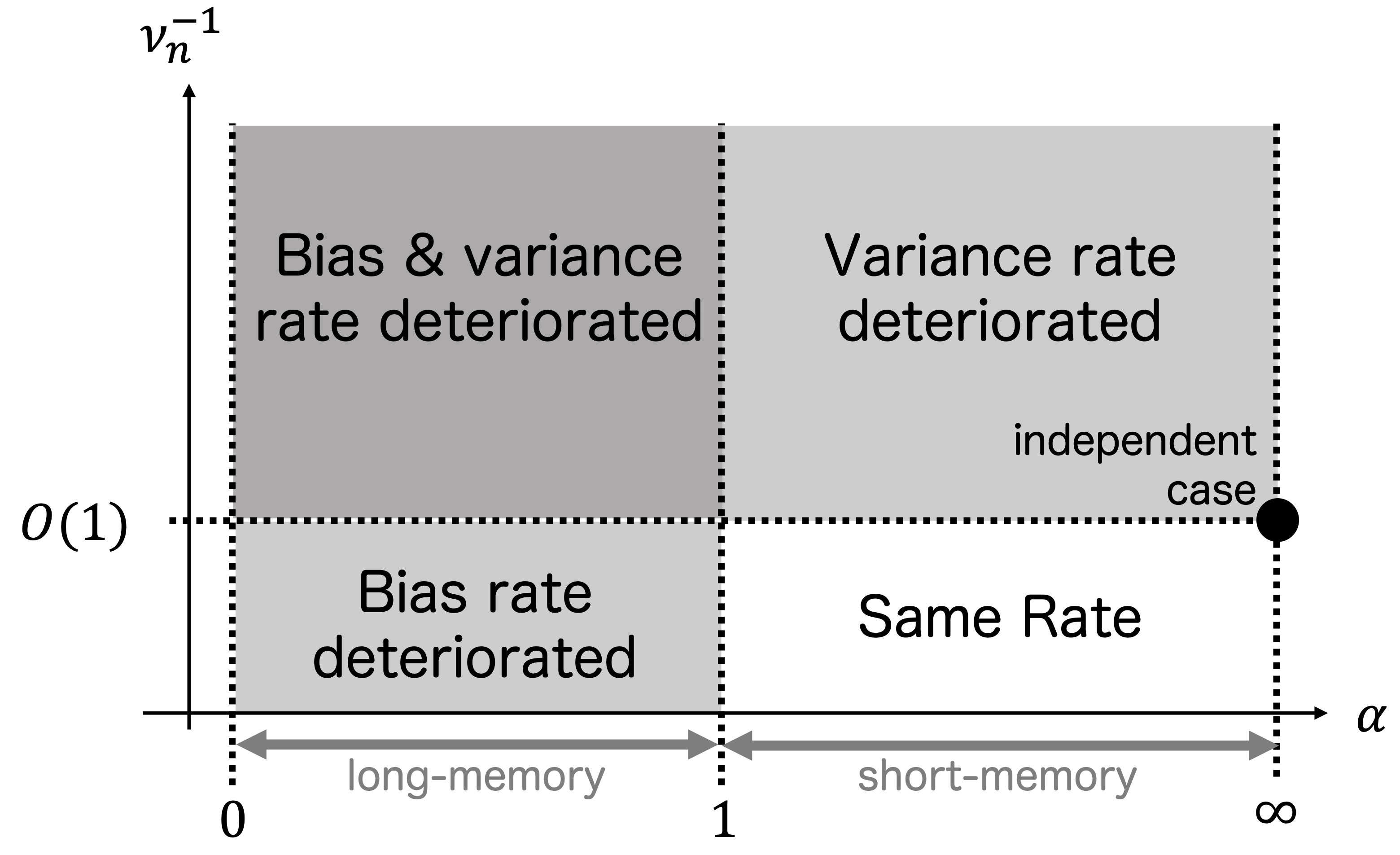
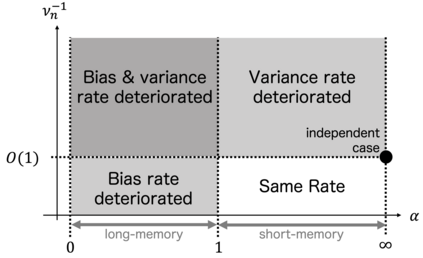
The success of large-scale models in recent years has increased the importance of statistical models with numerous parameters. Several studies have analyzed over-parameterized linear models with high-dimensional data that may not be sparse; however, existing results depend on the independent setting of samples. In this study, we analyze a linear regression model with dependent time series data under over-parameterization settings. We consider an estimator via interpolation and developed a theory for excess risk of the estimator under multiple dependence types. This theory can treat infinite-dimensional data without sparsity and handle long-memory processes in a unified manner. Moreover, we bound the risk in our theory via the integrated covariance and nondegeneracy of autocorrelation matrices. The results show that the convergence rate of risks with short-memory processes is identical to that of cases with independent data, while long-memory processes slow the convergence rate. We also present several examples of specific dependent processes that can be applied to our setting.