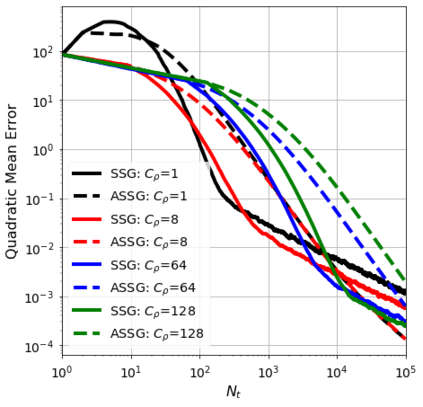
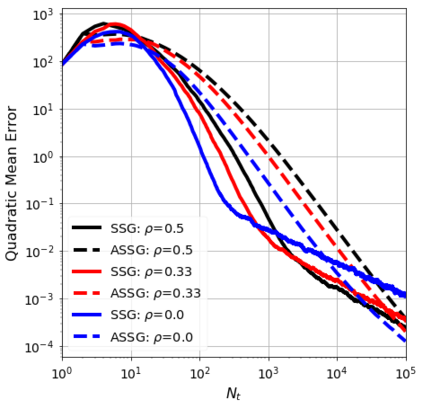
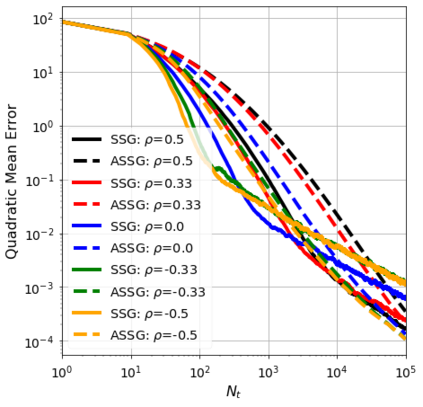
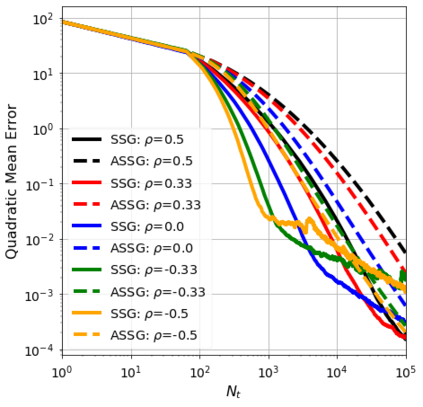
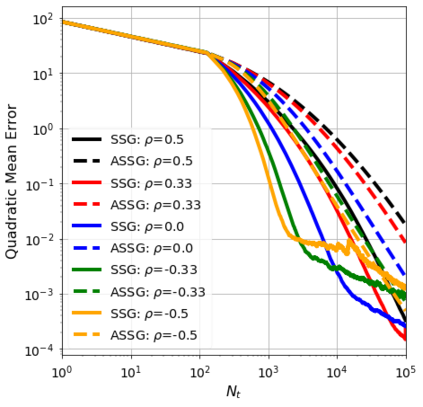
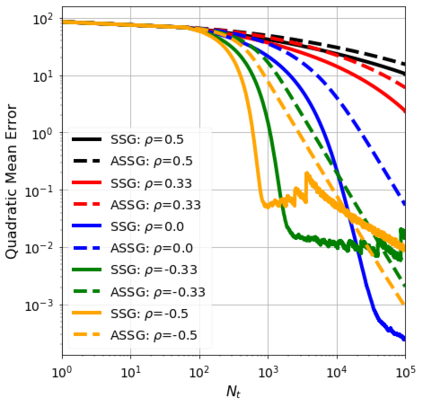
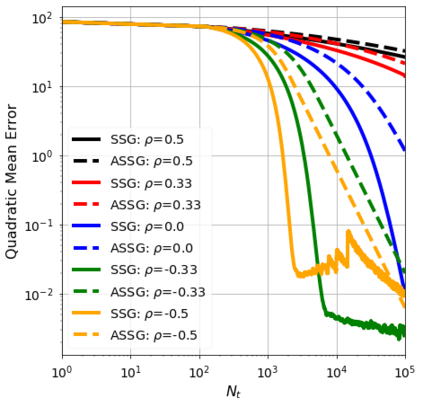
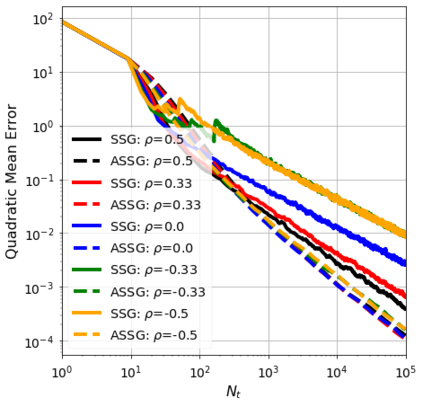
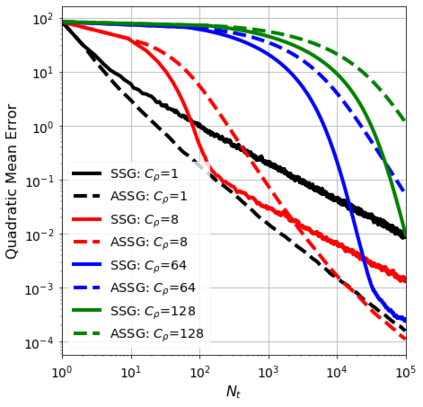
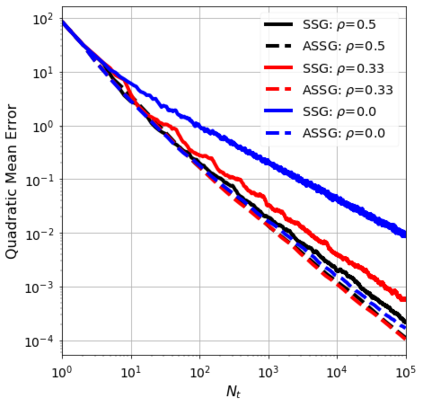
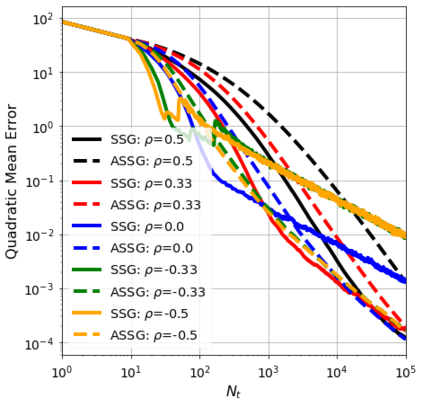
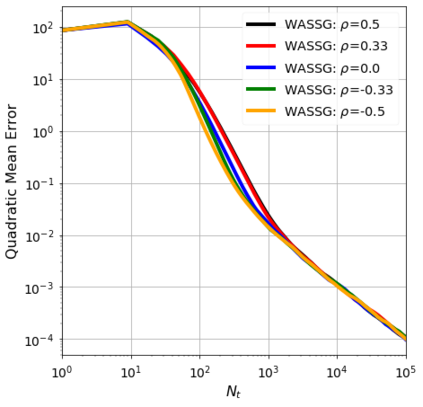
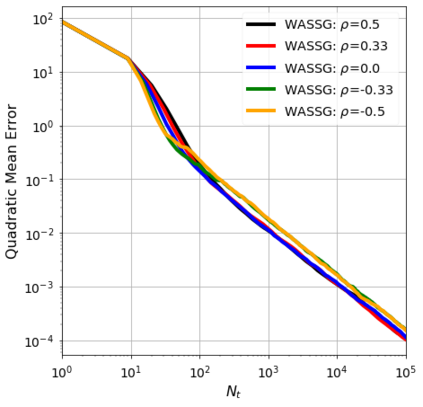
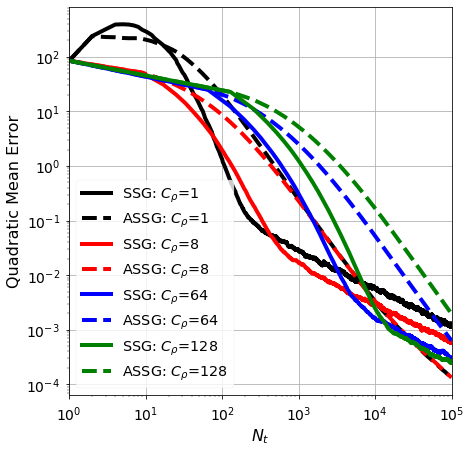
We consider the stochastic approximation problem in a streaming framework where an objective is minimized through unbiased estimates of its gradients. In this streaming framework, we consider time-varying data streams that must be processed sequentially. Our methods are Stochastic Gradient (SG) based due to their applicability and computational advantages. We provide a non-asymptotic analysis of the convergence of various SG-based methods; this includes the famous SG descent (a.k.a. Robbins-Monro algorithm), constant and time-varying mini-batch SG methods, and their averaged estimates (a.k.a. Polyak-Ruppert averaging). Our analysis suggests choosing the learning rate according to the expected data streams, which can speed up the convergence. In addition, we show how the averaged estimate can achieve optimal convergence in terms of attaining Cramer-Rao's lower bound while being robust to any data stream rate. In particular, our analysis shows how Polyak-Ruppert averaging of time-varying mini-batches can provide variance reduction and accelerate convergence simultaneously, which is advantageous for large-scale learning problems. These theoretical results are illustrated for various data streams, showing the effectiveness of the proposed algorithms.
翻译:我们在一个流流框架内考虑随机近似问题,在这个流流框架中,一个目标通过对其梯度的公正估计而最小化。在这个流流框架中,我们考虑必须按顺序处理的时间变化数据流。我们的方法是基于其适用性和计算优势的Stochatic Gradient(SG SG ) 。我们对各种基于SG的方法的趋同性进行非随机分析;这包括著名的SG基底(a.k.a.robins-Monro算法)、恒定和时间变化的小型泡泡SG方法及其平均估计(a.k.a.polyak-Ruppert平均),我们的分析建议根据预期的数据流选择学习率,这可以加速趋同。此外,我们展示了平均估计如何在达到Cramer-Rao较低的约束度的同时实现最佳趋同性,同时对任何数据流速率进行稳健。我们的分析特别表明,在时间变化的微型杯中,Polyak-Ruppert平均率如何减少差异,并同时加速趋同,这对于大规模学习数据来说是有利的。