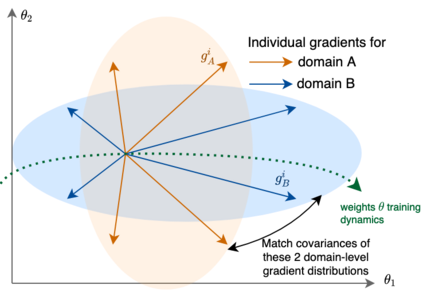
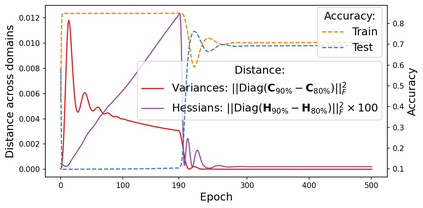
Learning robust models that generalize well under changes in the data distribution is critical for real-world applications. To this end, there has been a growing surge of interest to learn simultaneously from multiple training domains - while enforcing different types of invariance across those domains. Yet, all existing approaches fail to show systematic benefits under fair evaluation protocols. In this paper, we propose a new learning scheme to enforce domain invariance in the space of the gradients of the loss function: specifically, we introduce a regularization term that matches the domain-level variances of gradients across training domains. Critically, our strategy, named Fishr, exhibits close relations with the Fisher Information and the Hessian of the loss. We show that forcing domain-level gradient covariances to be similar during the learning procedure eventually aligns the domain-level loss landscapes locally around the final weights. Extensive experiments demonstrate the effectiveness of Fishr for out-of-distribution generalization. In particular, Fishr improves the state of the art on the DomainBed benchmark and performs significantly better than Empirical Risk Minimization. The code is released at https://github.com/alexrame/fishr.
翻译:在数据分配变化下广泛推广的强有力的学习模型对于现实世界应用至关重要。为此,人们越来越有兴趣同时从多个培训领域学习,同时在这些领域实施不同类型的差异。然而,所有现有方法都未能显示公平评估协议下的系统效益。在本文件中,我们提出一个新的学习计划,在损失函数的梯度空间中执行域差异性:具体地说,我们引入一个正规化术语,与不同培训领域的梯度的域级差异相匹配。关键是,我们的战略,名为Fisher,显示了与渔业信息和损失的赫斯仪的密切关系。我们显示,在学习过程中,迫使域级梯度变量相似,最终将最后重量周围的域级损失场景相匹配。广泛的实验表明,Fishercher对分配范围外的通用效果。特别是,Fisher改进了DomainBed基准的艺术状况,并比Emprical风险最小化要好得多。代码在 https://github.com/allamexe/fisher发布。