Parameter optimization for restarted mixed precision iterative sparse solver

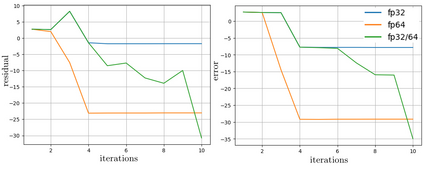
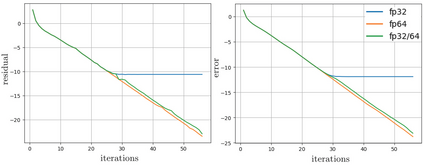
The problem of optimal precision switching for the conjugate gradient (CG) method applied to sparse linear systems is considered. A sparse matrix is defined as an $n\!\times\!n$ matrix with $m\!=\!O(n)$ nonzero entries. The algorithm first computes an approximate solution in single precision with tolerance $\varepsilon_1$, then switches to double precision to refine the solution to the required stopping tolerance $\varepsilon_2$. Based on estimates of system matrix parameters -- computed in time which does not exceed $1\%$ of the time needed to solve the system in double precision -- we determine the optimal value of $\varepsilon_1$ that minimizes total computation time. This value is obtained by classifying the matrix using the $k$-nearest neighbors method on a small precomputed sample. Classification relies on a feature vector comprising: the matrix size $n$, the number of nonzeros $m$, the pseudo-diameter of the matrix sparsity graph, and the average rate of residual norm decay during the early CG iterations in single precision. We show that, in addition to the matrix condition number, the diameter of the sparsity graph influences the growth of rounding errors during iterative computations. The proposed algorithm reduces the computational complexity of the CG -- expressed in equivalent double-precision iterations -- by more than $17\%$ on average across the considered matrix types in a sequential setting. The resulting speedup is at most $1.5\%$ worse than that achieved with the optimal (oracle) choice of $\varepsilon_1$. While the impact of matrix structure on Krylov subspace method convergence is well understood, the use of the sparsity graph diameter as a predictive feature for rounding error growth in mixed-precision CG appears to be novel. To the best of our knowledge, no prior work employs graph diameter to guide precision switching in iterative linear solvers.