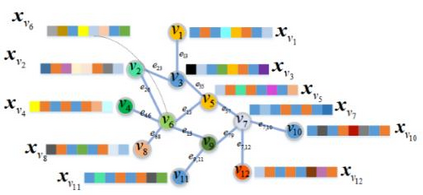
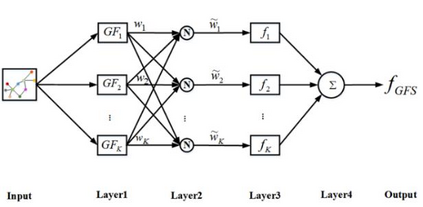
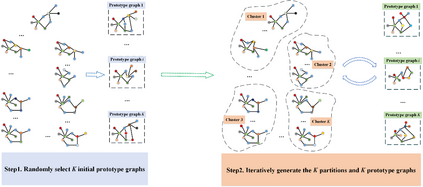
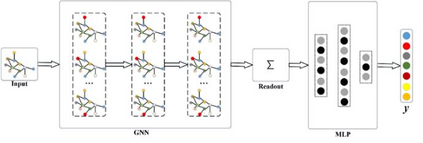
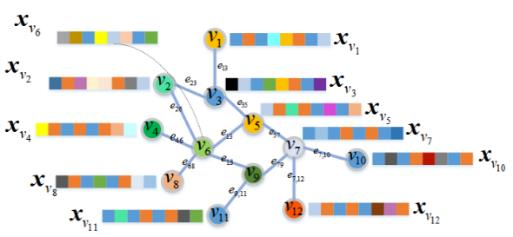
Fuzzy systems (FSs) have enjoyed wide applications in various fields, including pattern recognition, intelligent control, data mining and bioinformatics, which is attributed to the strong interpretation and learning ability. In traditional application scenarios, FSs are mainly applied to model Euclidean space data and cannot be used to handle graph data of non-Euclidean structure in nature, such as social networks and traffic route maps. Therefore, development of FS modeling method that is suitable for graph data and can retain the advantages of traditional FSs is an important research. To meet this challenge, a new type of FS for graph data modeling called Graph Fuzzy System (GFS) is proposed in this paper, where the concepts, modeling framework and construction algorithms are systematically developed. First, GFS related concepts, including graph fuzzy rule base, graph fuzzy sets and graph consequent processing unit (GCPU), are defined. A GFS modeling framework is then constructed and the antecedents and consequents of the GFS are presented and analyzed. Finally, a learning framework of GFS is proposed, in which a kernel K-prototype graph clustering (K2PGC) is proposed to develop the construction algorithm for the GFS antecedent generation, and then based on graph neural network (GNNs), consequent parameters learning algorithm is proposed for GFS. Specifically, three different versions of the GFS implementation algorithm are developed for comprehensive evaluations with experiments on various benchmark graph classification datasets. The results demonstrate that the proposed GFS inherits the advantages of both existing mainstream GNNs methods and conventional FSs methods while achieving better performance than the counterparts.
翻译:暂无翻译