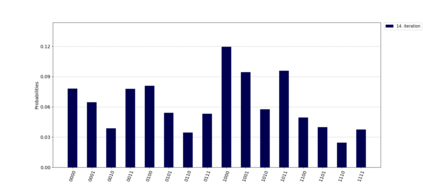
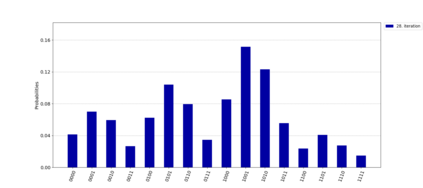
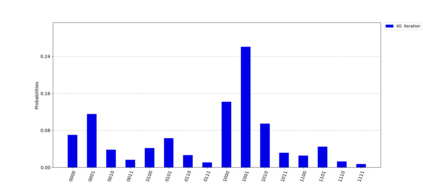
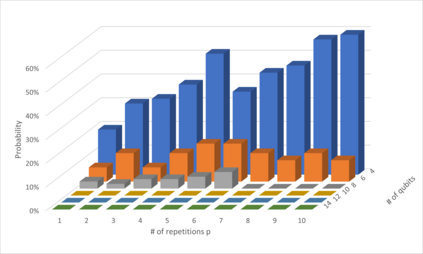
Quantum computing promises to solve difficult optimization problems in chemistry, physics and mathematics more efficiently than classical computers, but requires fault-tolerant quantum computers with millions of qubits. To overcome errors introduced by today's quantum computers, hybrid algorithms combining classical and quantum computers are used. In this paper we tackle the multiple query optimization problem (MQO) which is an important NP-hard problem in the area of data-intensive problems. We propose a novel hybrid classical-quantum algorithm to solve the MQO on a gate-based quantum computer. We perform a detailed experimental evaluation of our algorithm and compare its performance against a competing approach that employs a quantum annealer -- another type of quantum computer. Our experimental results demonstrate that our algorithm currently can only handle small problem sizes due to the limited number of qubits available on a gate-based quantum computer compared to a quantum computer based on quantum annealing. However, our algorithm shows a qubit efficiency of close to 99% which is almost a factor of 2 higher compared to the state of the art implementation. Finally, we analyze how our algorithm scales with larger problem sizes and conclude that our approach shows promising results for near-term quantum computers.
翻译:量子计算有望比古典计算机更高效地解决化学、物理和数学方面的最优化难题,但需要使用数百万夸比特的防过错量计算机。 要克服今天量子计算机引入的错误,就要使用混合算法,同时使用古典和量子计算机。 在本文中,我们处理数据密集型领域一个重要的NP硬性问题,即多盘量优化问题。我们提议一种新型的混合古典-夸特姆算法,在以门基量子计算机上解决MQO。我们详细实验了我们的算法,并将其性能与使用量子麻醉器 -- -- 另一种量子计算机 -- -- 的竞争性方法相比较。我们的实验结果显示,由于基于门基量子计算机的可使用量子数量有限,我们的算法目前只能处理小问题大小,而与基于量子肾脏的量计算机相比,我们的量子计算法则显示接近99%,这与艺术实施状态相比几乎高出2倍。最后,我们分析了我们使用较大问题大小的算法规模,我们得出了我们接近量子的算法的结果。