A Unified Algorithm Framework for Unsupervised Discovery of Skills based on Determinantal Point Process

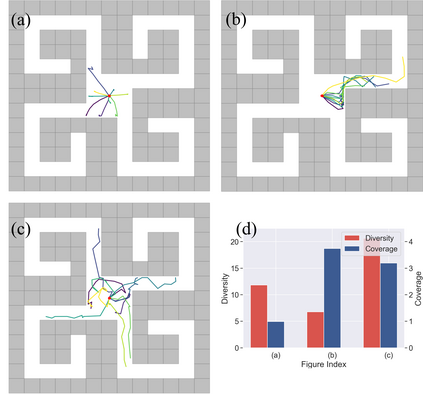
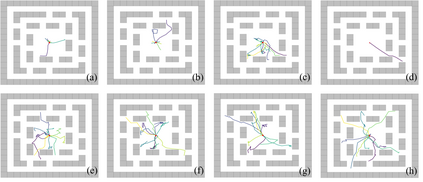
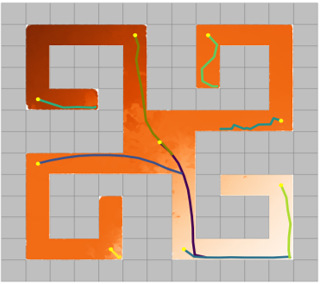
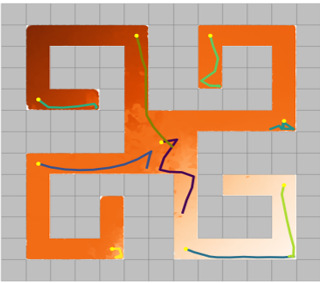
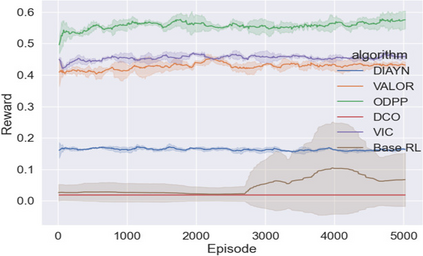
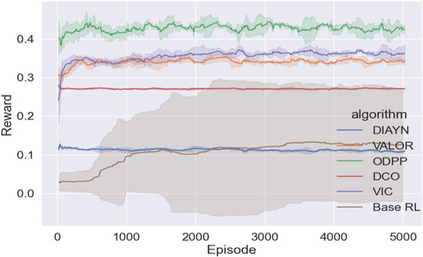
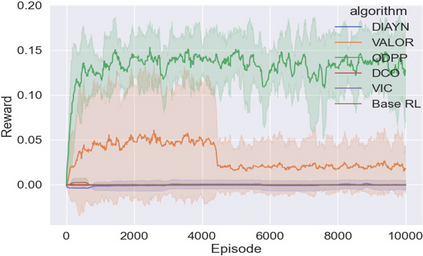
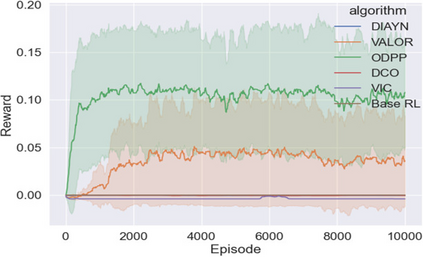
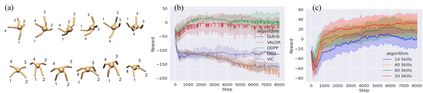
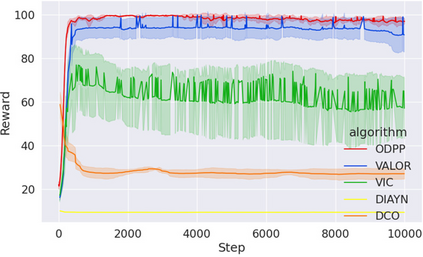
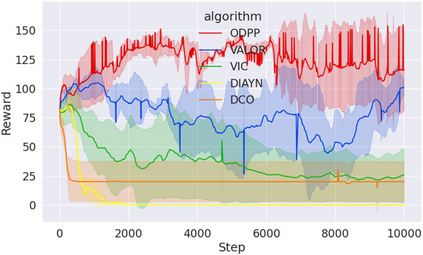
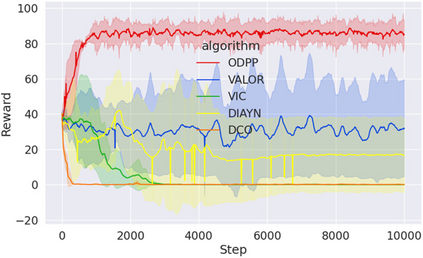
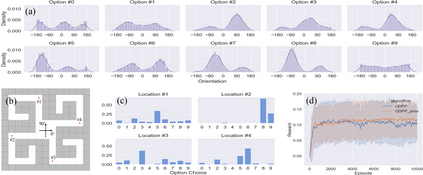
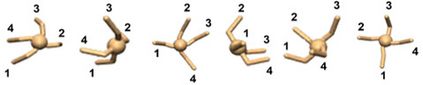
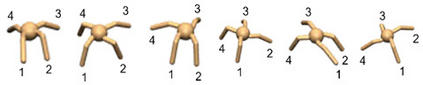
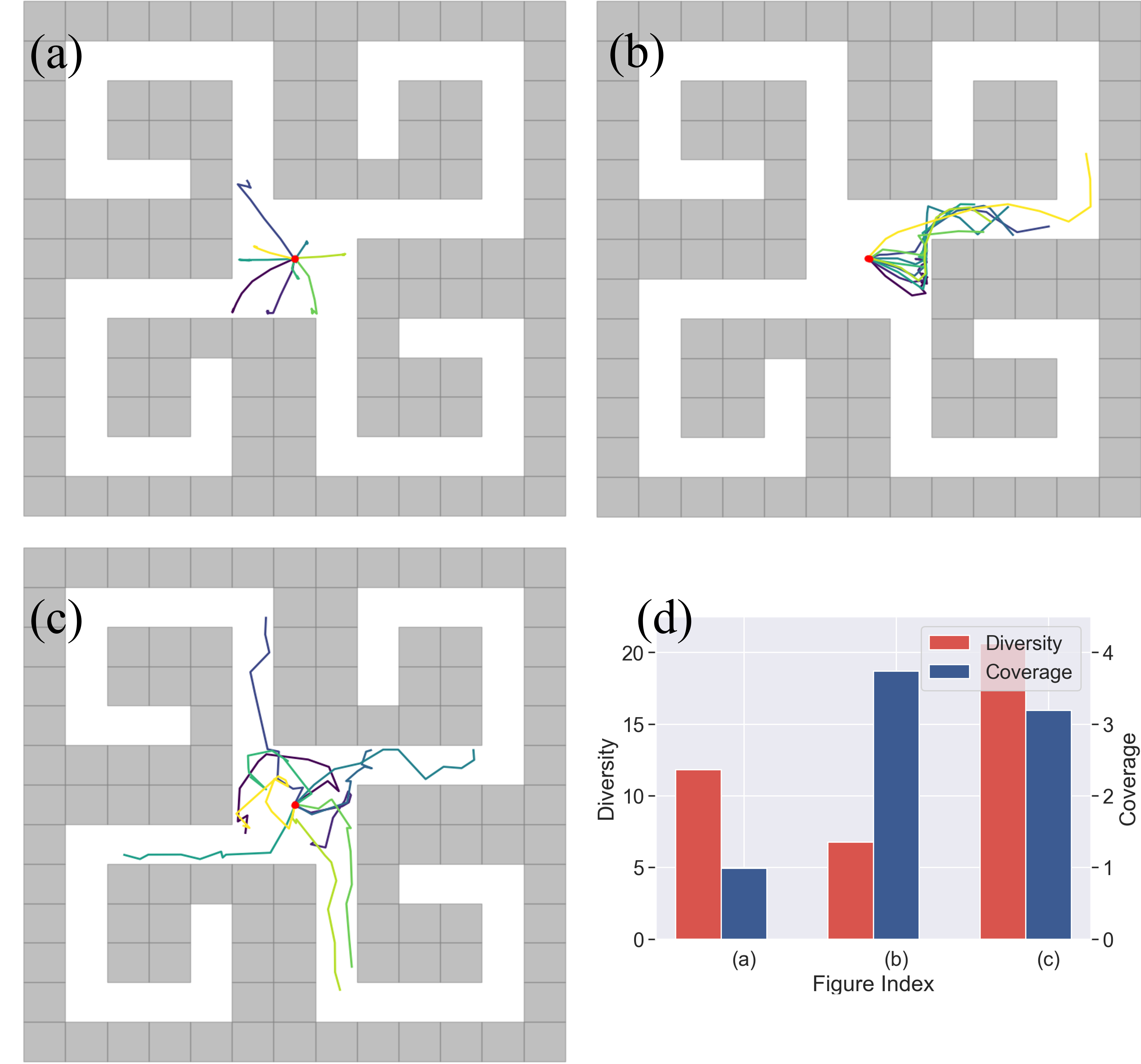
Learning rich skills through temporal abstractions without supervision of external rewards is at the frontier of Reinforcement Learning research. Existing works mainly fall into two distinctive categories: variational and Laplacian-based skill (a.k.a., option) discovery. The former maximizes the diversity of the discovered options through a mutual information loss but overlooks coverage of the state space, while the latter focuses on improving the coverage of options by increasing connectivity during exploration, but does not consider diversity. In this paper, we propose a unified framework that quantifies diversity and coverage through a novel use of the Determinantal Point Process (DPP) and enables unsupervised option discovery explicitly optimizing both objectives. Specifically, we define the DPP kernel matrix with the Laplacian spectrum of the state transition graph and use the expected mode number in the trajectories as the objective to capture and enhance both diversity and coverage of the learned options. The proposed option discovery algorithm is extensively evaluated using challenging tasks built with Mujoco and Atari, demonstrating that our proposed algorithm substantially outperforms SOTA baselines from both diversity- and coverage-driven categories. The codes are available at https://github.com/LucasCJYSDL/ODPP.