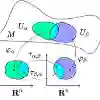
Information geometry is a study of statistical manifolds, that is, spaces of probability distributions from a geometric perspective. Its classical information-theoretic applications relate to statistical concepts such as Fisher information, sufficient statistics, and efficient estimators. Today, information geometry has emerged as an interdisciplinary field that finds applications in diverse areas such as radar sensing, array signal processing, quantum physics, deep learning, and optimal transport. This article presents an overview of essential information geometry to initiate an information theorist, who may be unfamiliar with this exciting area of research. We explain the concepts of divergences on statistical manifolds, generalized notions of distances, orthogonality, and geodesics, thereby paving the way for concrete applications and novel theoretical investigations. We also highlight some recent information-geometric developments, which are of interest to the broader information theory community.
翻译:暂无翻译