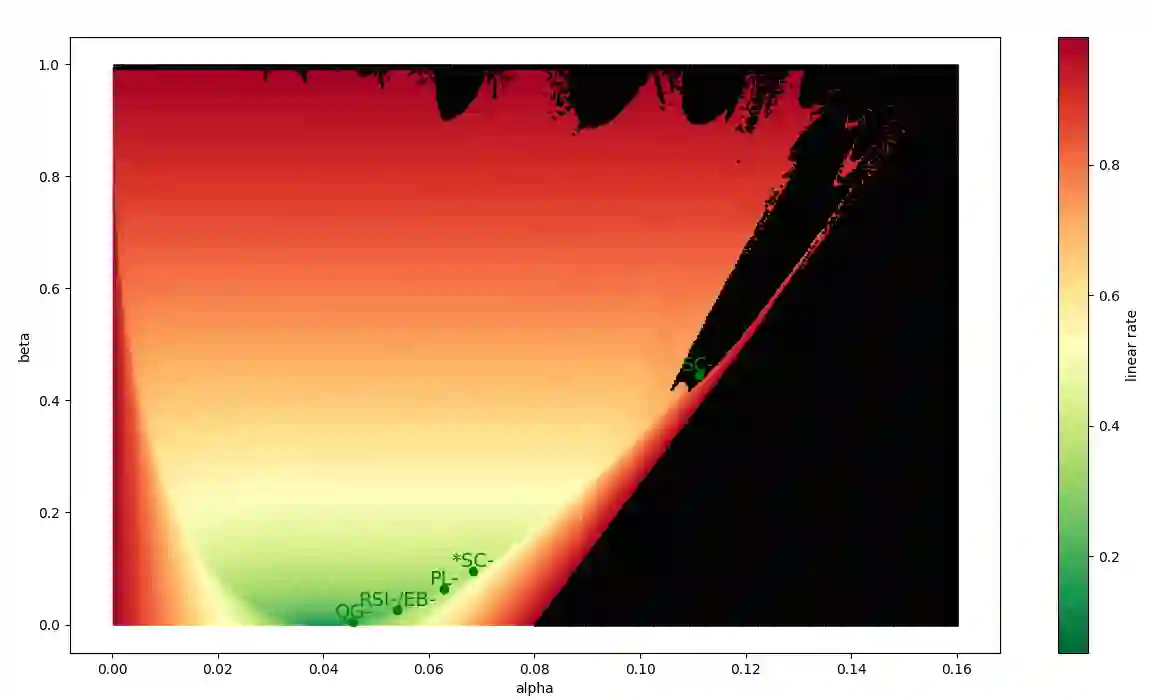
The study of first-order optimization algorithms (FOA) typically starts with assumptions on the objective functions, most commonly smoothness and strong convexity. These metrics are used to tune the hyperparameters of FOA. We introduce a class of perturbations quantified via a new norm, called *-norm. We show that adding a small perturbation to the objective function has an equivalently small impact on the behavior of any FOA, which suggests that it should have a minor impact on the tuning of the algorithm. However, we show that smoothness and strong convexity can be heavily impacted by arbitrarily small perturbations, leading to excessively conservative tunings and convergence issues. In view of these observations, we propose a notion of continuity of the metrics, which is essential for a robust tuning strategy. Since smoothness and strong convexity are not continuous, we propose a comprehensive study of existing alternative metrics which we prove to be continuous. We describe their mutual relations and provide their guaranteed convergence rates for the Gradient Descent algorithm accordingly tuned. Finally we discuss how our work impacts the theoretical understanding of FOA and their performances.
翻译:对一阶优化算法(FOA)的研究通常从对客观功能的假设开始,最通常的平稳和强烈的调和。这些衡量标准被用来调和FOA的超参数。我们引入了通过称为 *- 规范的新规范量化的一类扰动。我们表明,对目标函数增加小扰动对任何FOA的行为都具有相当小的影响,这表明它对算法的调适应产生微小的影响。然而,我们表明,任意的小扰动会严重影响到光滑和强烈的融和,导致过度保守的调和和趋同问题。根据这些观察,我们提出了一套衡量标准连续性的概念,这对稳健的调适战略至关重要。由于光滑和强烈的调和不连续,我们建议对现有替代指标进行全面研究,我们证明它们是连续的。我们描述了它们之间的相互关系,并提供了它们保证的趋同率,以便最终对梯层算法进行调整。我们最后讨论了我们的工作如何影响FOA的理论理解及其性。