The Effect of Intrinsic Dimension on Metric Learning under Compression

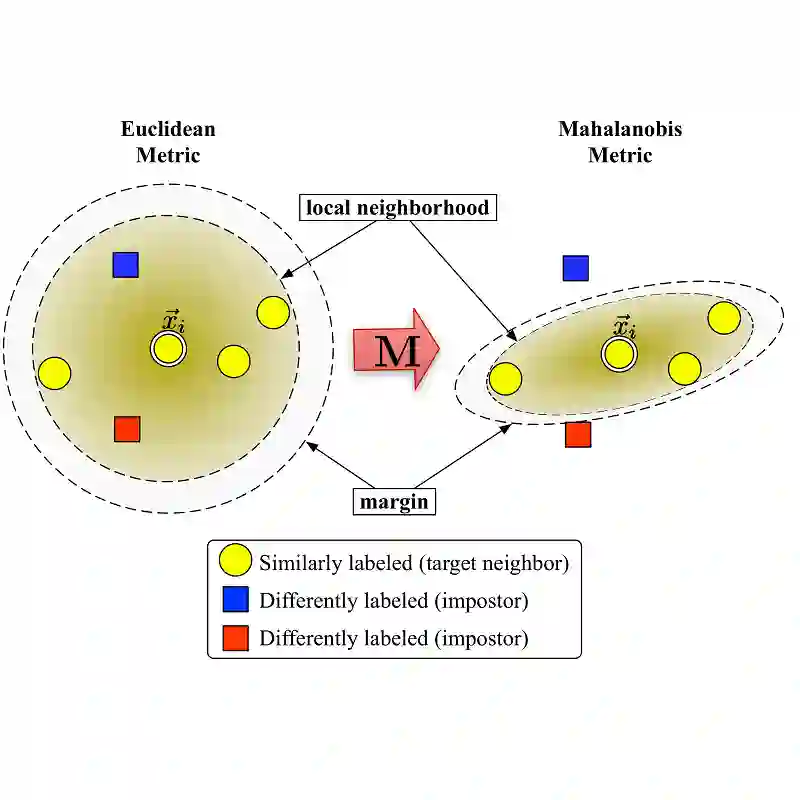
Metric learning aims at finding a suitable distance metric over the input space, to improve the performance of distance-based learning algorithms. In high-dimensional settings, metric learning can also play the role of dimensionality reduction, by imposing a low-rank restriction to the learnt metric. In this paper, instead of training a low-rank metric on high-dimensional data, we consider a randomly compressed version of the data, and train a full-rank metric there. We give theoretical guarantees on the error of distance-based metric learning, with respect to the random compression, which do not depend on the ambient dimension. Our bounds do not make any explicit assumptions, aside from i.i.d. data from a bounded support, and automatically tighten when benign geometrical structures are present. Experimental results on both synthetic and real data sets support our theoretical findings in high-dimensional settings.