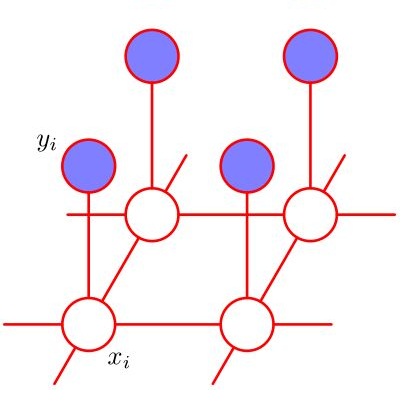
We derive an explicit link between Gaussian Markov random fields on metric graphs and graphical models, and in particular show that a Markov random field restricted to the vertices of the graph is, under mild regularity conditions, a Gaussian graphical model with a distribution which is faithful to its pairwise independence graph, which coincides with the neighbor structure of the metric graph. This is used to show that there are no Gaussian random fields on general metric graphs which are both Markov and isotropic in some suitably regular metric on the graph, such as the geodesic or resistance metrics.
翻译:暂无翻译
相关内容
专知会员服务
54+阅读 · 2020年1月30日
专知会员服务
34+阅读 · 2020年1月15日
专知会员服务
34+阅读 · 2019年10月18日
专知会员服务
36+阅读 · 2019年10月17日
Arxiv
15+阅读 · 2021年5月19日
Arxiv
12+阅读 · 2021年5月7日
Arxiv
100+阅读 · 2020年2月20日
Arxiv
11+阅读 · 2019年9月8日
Arxiv
40+阅读 · 2019年6月4日
Arxiv
10+阅读 · 2018年3月20日