Polynomials shrinkage estimators of a multivariate normal mean

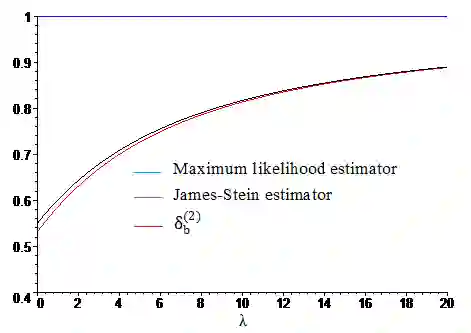
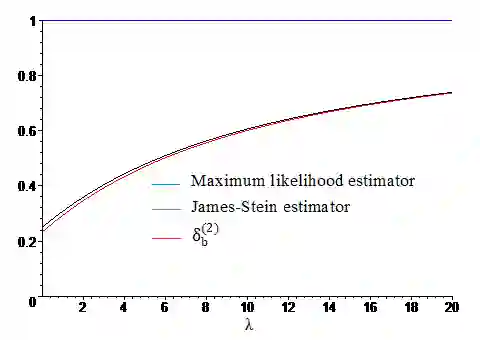
In this work, the estimation of the multivariate normal mean by different classes of shrinkage estimators is investigated. The risk associated with the balanced loss function is used to compare two estimators. We start by considering estimators that generalize the James-Stein estimator and show that these estimators dominate the maximum likelihood estimator (MLE), therefore are minimax, when the shrinkage function satisfies some conditions. Then, we treat estimators of polynomial form and prove the increase of the degree of the polynomial allows us to build a better estimator from the one previously constructed.