NN2Poly: A polynomial representation for deep feed-forward artificial neural networks

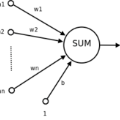
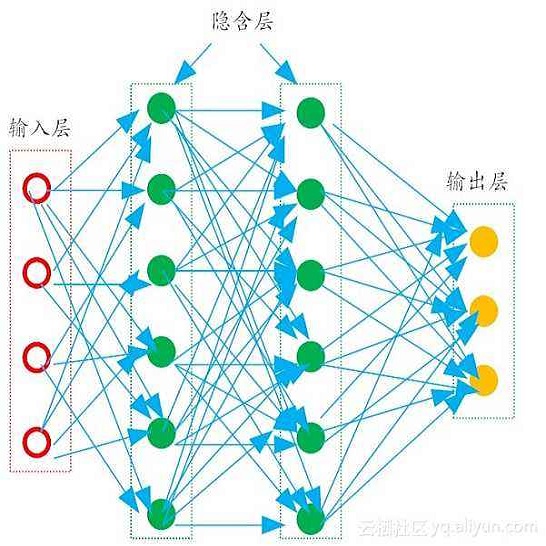
Interpretability of neural networks and their underlying theoretical behaviour remain an open field of study even after the great success of their practical applications, particularly with the emergence of deep learning. In this work, NN2Poly is proposed: a theoretical approach to obtain an explicit polynomial model that provides an accurate representation of an already trained fully-connected feed-forward artificial neural network (a multilayer perceptron or MLP). This approach extends a previous idea proposed in the literature, which was limited to single hidden layer networks, to work with arbitrarily deep MLPs in both regression and classification tasks. The objective of this paper is to achieve this by using a Taylor expansion on the activation function, at each layer, and then using several combinatorial properties to calculate the coefficients of the desired polynomials. Discussion is presented on the main computational challenges of this method, and the way to overcome them by imposing certain constraints during the training phase. Finally, simulation experiments as well as an application to a real data set are presented to demonstrate the effectiveness of the proposed method.