Neural Networks Base on Power Method and Inverse Power Method for Solving Linear Eigenvalue Problems

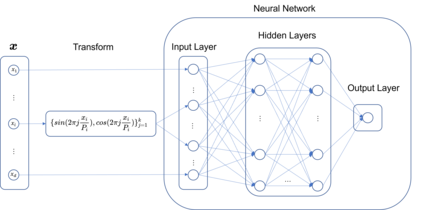
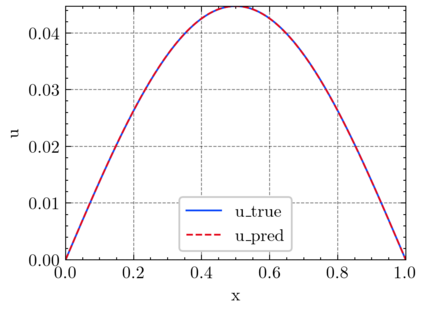
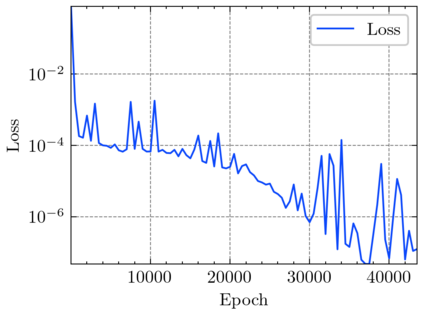
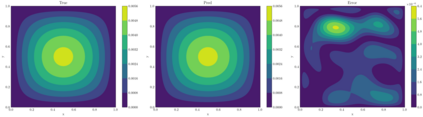
In this article, we propose three methods Power Method Neural Network (PMNN), Inverse Power Method Neural Networ (IPMNN) and Shifted Inverse Power Method Neural Network (SIPMNN) combined with power method, inverse power method and shifted inverse power method to solve eigenvalue problems with the dominant eigenvalue, the smallest eigenvalue and the smallest zero eigenvalue, respectively. The methods share similar spirits with traditional methods, but the differences are the differential operator realized by Automatic Differentiation (AD), the eigenfunction learned by the neural network and the iterations implemented by optimizing the specially defined loss function. We examine the applicability and accuracy of our methods in several numerical examples in high dimensions. Numerical results obtained by our methods for multidimensional problems show that our methods can provide accurate eigenvalue and eigenfunction approximations.