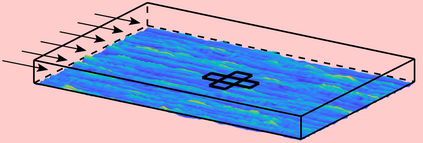
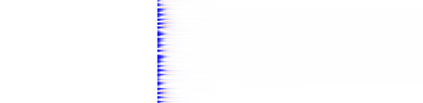
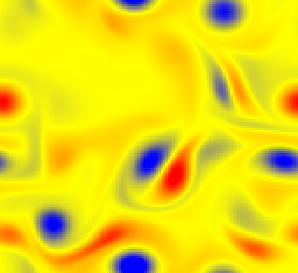
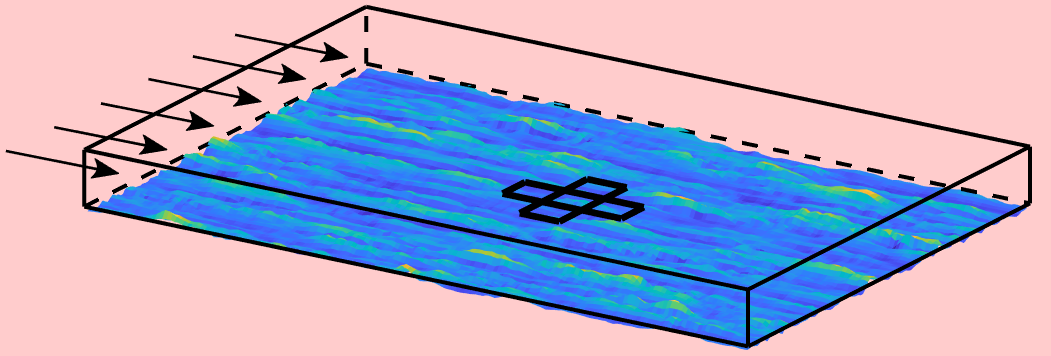
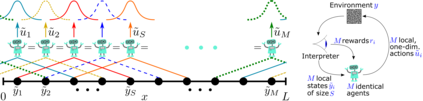We present a convolutional framework which significantly reduces the complexity and thus, the computational effort for distributed reinforcement learning control of dynamical systems governed by partial differential equations (PDEs). Exploiting translational invariances, the high-dimensional distributed control problem can be transformed into a multi-agent control problem with many identical, uncoupled agents. Furthermore, using the fact that information is transported with finite velocity in many cases, the dimension of the agents' environment can be drastically reduced using a convolution operation over the state space of the PDE. In this setting, the complexity can be flexibly adjusted via the kernel width or by using a stride greater than one. Moreover, scaling from smaller to larger systems -- or the transfer between different domains -- becomes a straightforward task requiring little effort. We demonstrate the performance of the proposed framework using several PDE examples with increasing complexity, where stabilization is achieved by training a low-dimensional deep deterministic policy gradient agent using minimal computing resources.
翻译:我们提出了一个共变框架,大大降低了复杂性,从而大大降低了对受部分差异方程(PDEs)制约的动态系统进行分布式强化学习控制的计算努力。 开发翻译差异,高维分布式控制问题可以转化成多剂控制问题,许多相同、非混合的物剂都存在。 此外,利用信息在很多情况下以有限速度传输这一事实,在PDE的状态空间上进行递增操作,可以大幅降低物剂环境的维度。在这种环境下,可以通过内核宽度或通过使用大于1的步子灵活调整其复杂性。此外,从小到大系统,或在不同领域之间的转移,成为一项简单的任务。我们用一些复杂程度越来越高的PDE实例展示了拟议框架的绩效,通过使用最小的计算资源培训低维深度的确定性政策梯度剂,从而实现了稳定性。