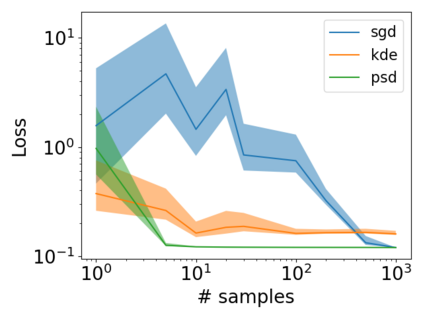
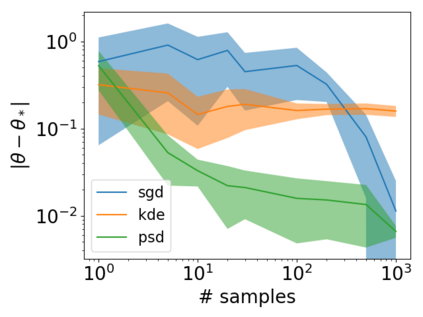
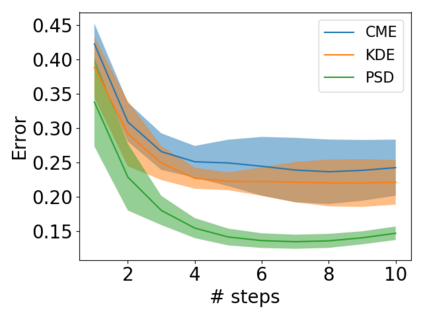
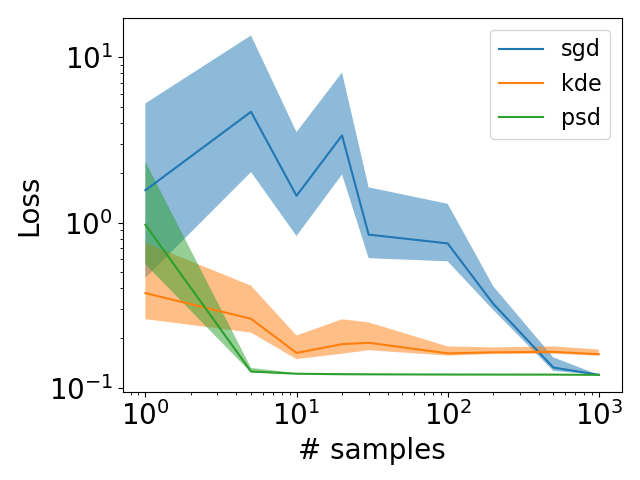
Finding a good way to model probability densities is key to probabilistic inference. An ideal model should be able to concisely approximate any probability, while being also compatible with two main operations: multiplications of two models (product rule) and marginalization with respect to a subset of the random variables (sum rule). In this work, we show that a recently proposed class of positive semi-definite (PSD) models for non-negative functions is particularly suited to this end. In particular, we characterize both approximation and generalization capabilities of PSD models, showing that they enjoy strong theoretical guarantees. Moreover, we show that we can perform efficiently both sum and product rule in closed form via matrix operations, enjoying the same versatility of mixture models. Our results open the way to applications of PSD models to density estimation, decision theory and inference. Preliminary empirical evaluation supports our findings.
翻译:模拟概率密度的好方法是概率推论的关键。理想模型应该能够简洁地估计任何概率,同时与两个主要操作兼容:两种模型的倍增(产品规则)和随机变量子集的边缘化(总规则)。在这项工作中,我们表明最近提议的非负函数正半确定性模型类别特别适合这一目的。我们特别将私营部门司模型的近似和概括性能力定性为两种能力,表明它们享有很强的理论保证。此外,我们表明,我们可以通过矩阵操作以封闭的形式有效地执行总和和产品规则,享受同样的混合模型的多功能。我们的结果为私营部门司模型应用密度估计、决定理论和推论开辟了道路。初步经验评价支持我们的调查结果。