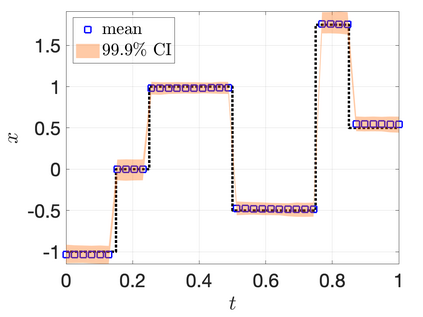
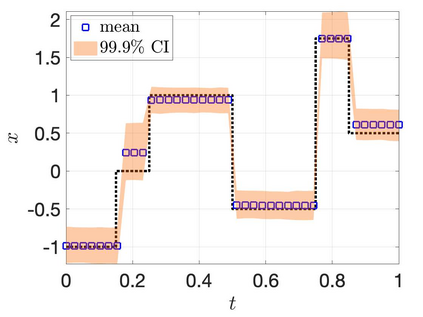
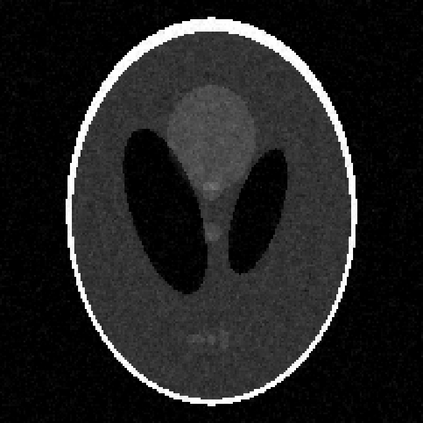
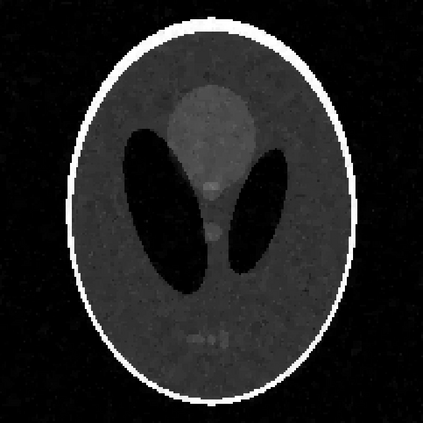
Image reconstruction based on indirect, noisy, or incomplete data remains an important yet challenging task. While methods such as compressive sensing have demonstrated high-resolution image recovery in various settings, there remain issues of robustness due to parameter tuning. Moreover, since the recovery is limited to a point estimate, it is impossible to quantify the uncertainty, which is often desirable. Due to these inherent limitations, a sparse Bayesian learning approach is sometimes adopted to recover a posterior distribution of the unknown. Sparse Bayesian learning assumes that some linear transformation of the unknown is sparse. However, most of the methods developed are tailored to specific problems, with particular forward models and priors. Here, we present a generalized approach to sparse Bayesian learning. It has the advantage that it can be used for various types of data acquisitions and prior information. Some preliminary results on image reconstruction/recovery indicate its potential use for denoising, deblurring, and magnetic resonance imaging.
翻译:基于间接、吵闹或不完整数据的图像重建仍是一项重要但具有挑战性的任务。尽管压缩遥感等方法显示在不同环境中的高分辨率图像恢复情况,但由于参数调整,还存在稳健性问题。此外,由于恢复仅限于点数估计,因此无法量化不确定性,而这往往是可取的。由于这些内在的局限性,有时会采取稀疏的巴耶斯学习方法来恢复未知的后传分布。浅浅浅的巴耶斯人学习假设未知的某种线性转变是少之又少。然而,所开发的大多数方法都是针对具体问题而设计的,特别是前期模型和前期模型。在这里,我们介绍了稀有的巴耶斯人学习的普遍方法。它的好处是,它可以用于各种类型的数据采集和先前的信息。关于图像重建/恢复的一些初步结果显示,它有可能用于去鼻、脱泡和磁共振成像。