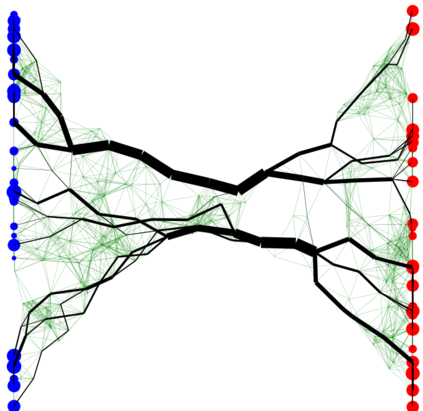
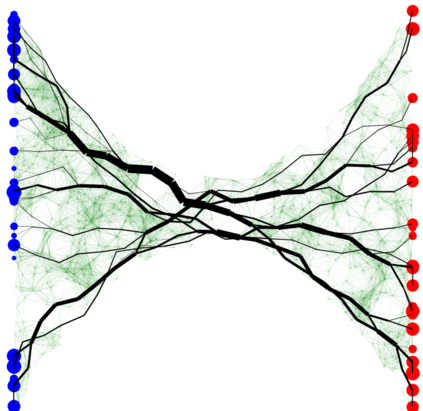
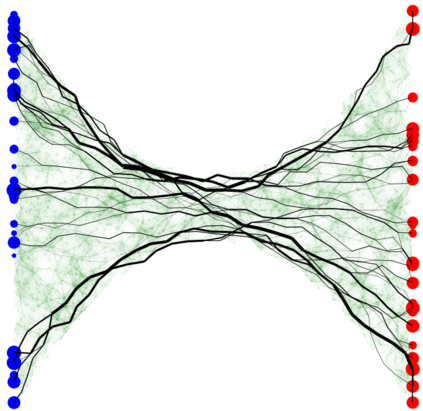
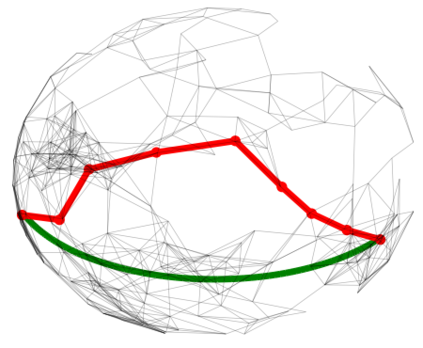
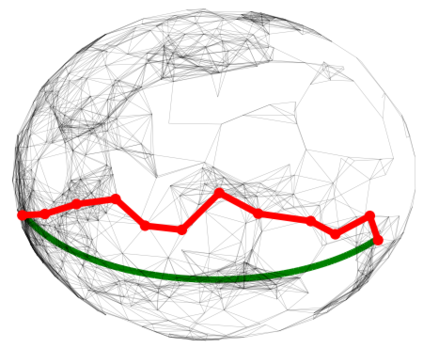
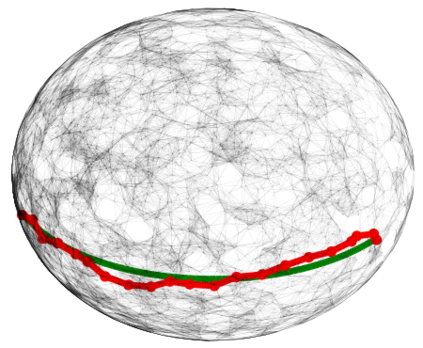
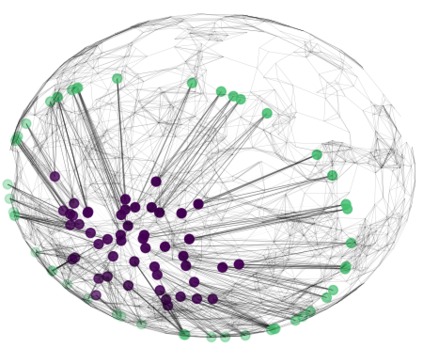
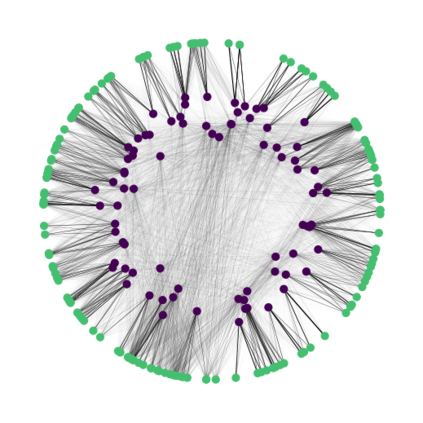
In graph analysis, a classic task consists in computing similarity measures between (groups of) nodes. In latent space random graphs, nodes are associated to unknown latent variables. One may then seek to compute distances directly in the latent space, using only the graph structure. In this paper, we show that it is possible to consistently estimate entropic-regularized Optimal Transport (OT) distances between groups of nodes in the latent space. We provide a general stability result for entropic OT with respect to perturbations of the cost matrix. We then apply it to several examples of random graphs, such as graphons or $\epsilon$-graphs on manifolds. Along the way, we prove new concentration results for the so-called Universal Singular Value Thresholding estimator, and for the estimation of geodesic distances on a manifold.
翻译:在图形分析中,经典的任务包括计算(各)节点之间的相似度量。在潜伏空间随机图中,节点与未知的潜伏变量相关。然后,人们可以试图直接计算潜伏空间的距离,只使用图形结构。在本文中,我们表明,可以一致估计潜伏空间各节点组之间的典型最佳迁移(OT)距离。我们在成本矩阵的扰动方面为 entro OT 提供了一个总体稳定性结果。然后,我们将它应用到几个随机图解的例子中,例如图解或元件上的 $\ epsilon$-graph 。沿着这段路上,我们证明所谓的通用成象值占定点数和估计多元上的地德距离的新浓度结果。