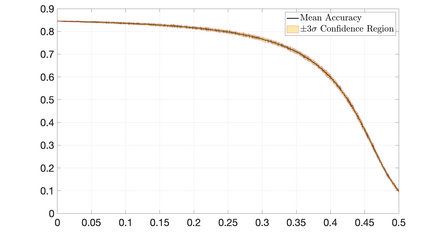
This paper studies the geometry of binary hyperdimensional computing (HDC), a computational scheme in which data are encoded using high-dimensional binary vectors. We establish a result about the similarity structure induced by the HDC binding operator and show that the Laplace kernel naturally arises in this setting, motivating our new encoding method Laplace-HDC, which improves upon previous methods. We describe how our results indicate limitations of binary HDC in encoding spatial information from images and discuss potential solutions, including using Haar convolutional features and the definition of a translation-equivariant HDC encoding. Several numerical experiments highlighting the improved accuracy of Laplace-HDC in contrast to alternative methods are presented. We also numerically study other aspects of the proposed framework such as robustness and the underlying translation-equivariant encoding.
翻译:暂无翻译