Disentanglement of Correlated Factors via Hausdorff Factorized Support

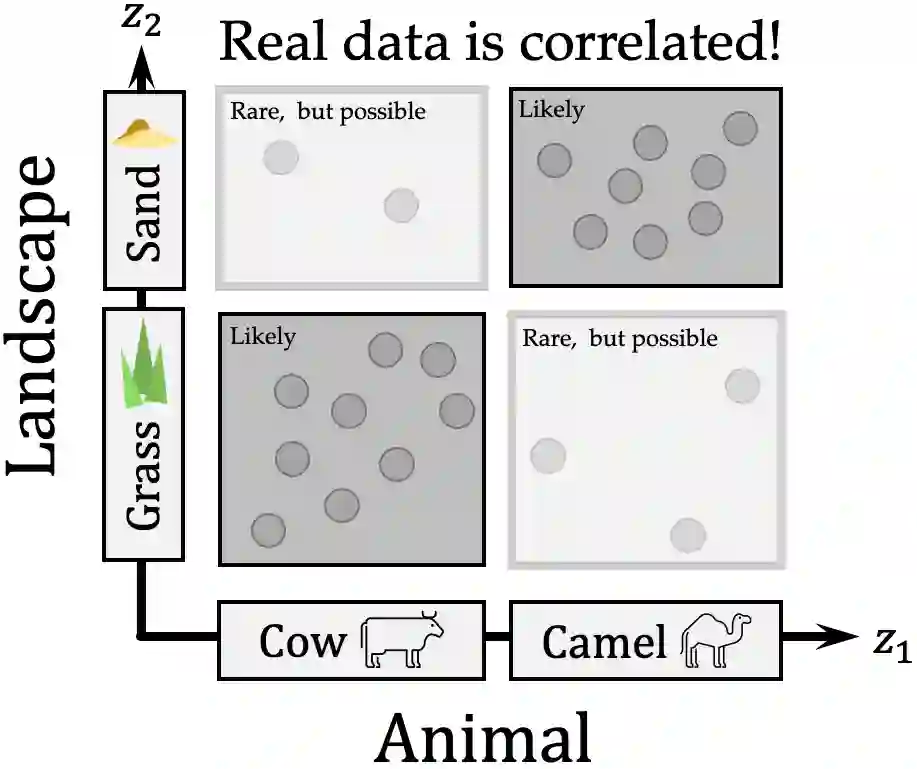
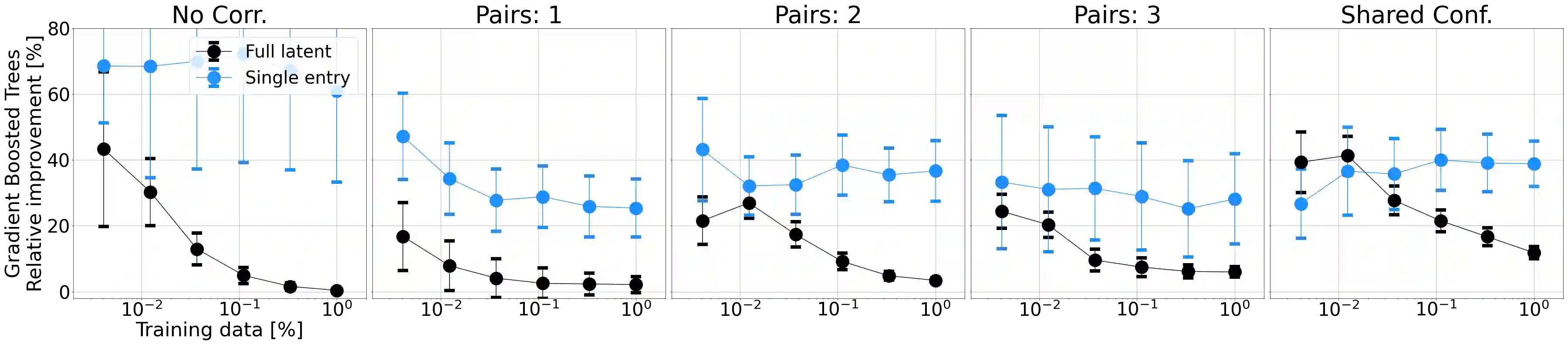
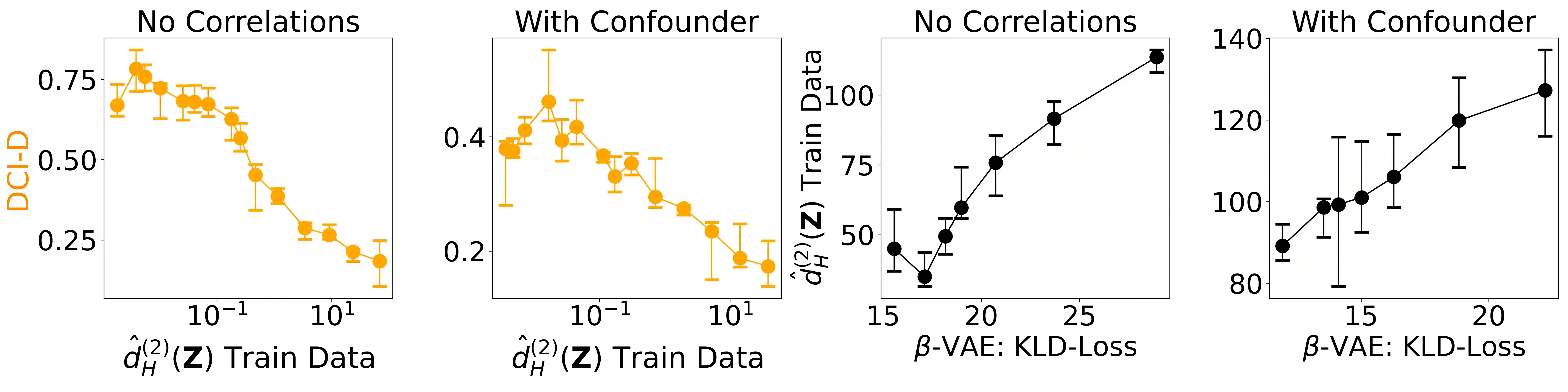
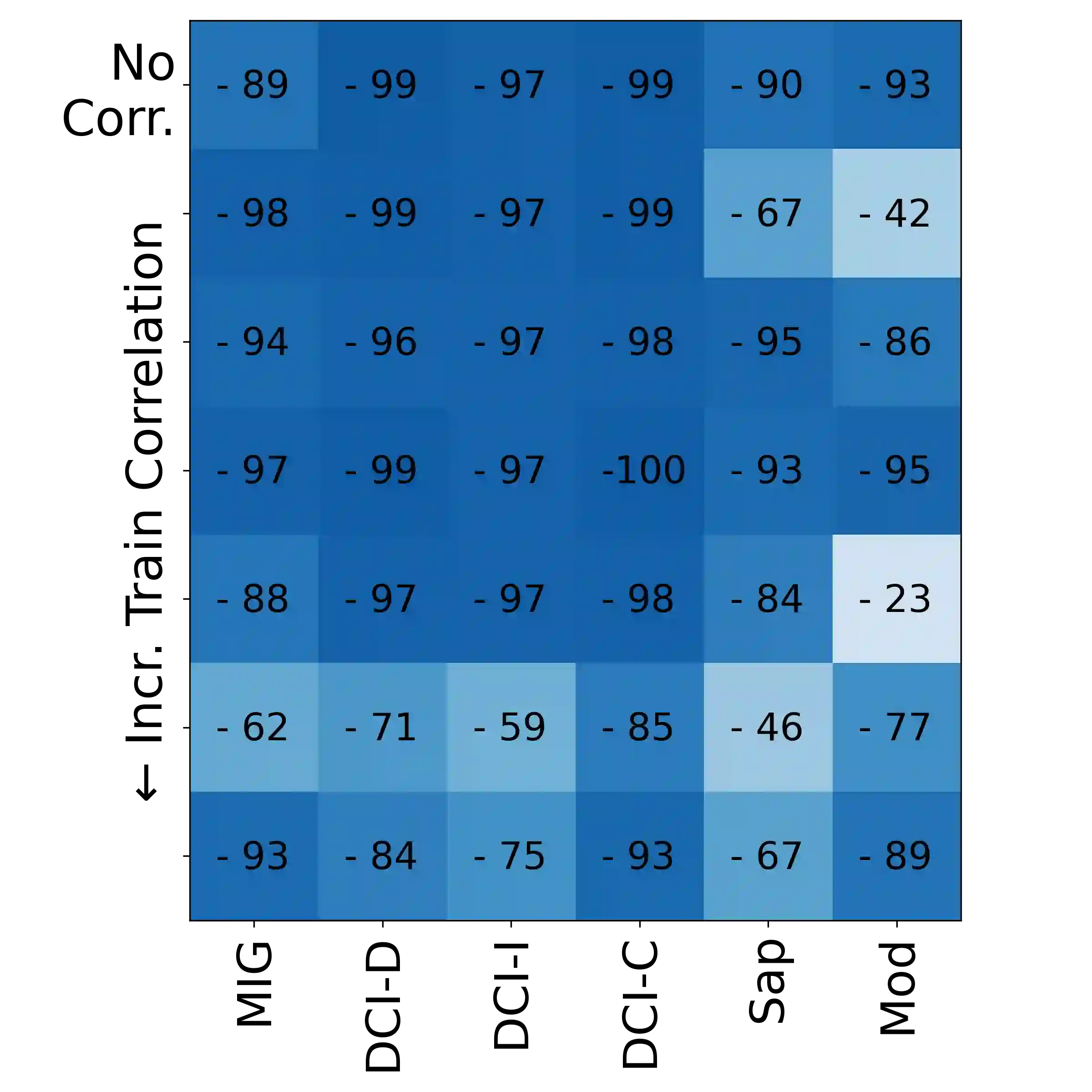
A grand goal in deep learning research is to learn representations capable of generalizing across distribution shifts. Disentanglement is one promising direction aimed at aligning a models representations with the underlying factors generating the data (e.g. color or background). Existing disentanglement methods, however, rely on an often unrealistic assumption: that factors are statistically independent. In reality, factors (like object color and shape) are correlated. To address this limitation, we propose a relaxed disentanglement criterion - the Hausdorff Factorized Support (HFS) criterion - that encourages a factorized support, rather than a factorial distribution, by minimizing a Hausdorff distance. This allows for arbitrary distributions of the factors over their support, including correlations between them. We show that the use of HFS consistently facilitates disentanglement and recovery of ground-truth factors across a variety of correlation settings and benchmarks, even under severe training correlations and correlation shifts, with in parts over +60% in relative improvement over existing disentanglement methods. In addition, we find that leveraging HFS for representation learning can even facilitate transfer to downstream tasks such as classification under distribution shifts. We hope our original approach and positive empirical results inspire further progress on the open problem of robust generalization.