phi-FEM for the heat equation: optimal convergence on unfitted meshes in space

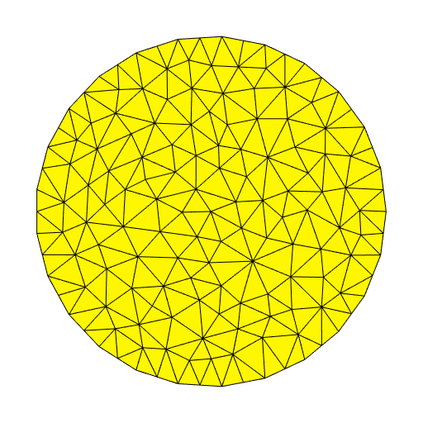
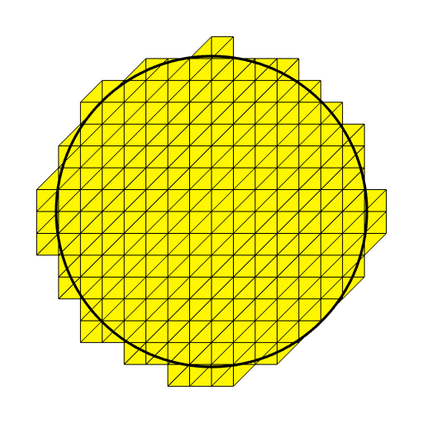
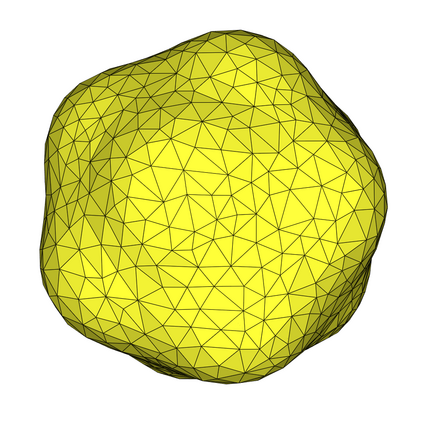
Thanks to a finite element method, we solve numerically parabolic partial differential equations on complex domains by avoiding the mesh generation, using a regular background mesh, not fitting the domain and its real boundary exactly. Our technique follows the phi-FEM paradigm, which supposes that the domain is given by a level-set function. In this paper, we prove a priori error estimates in l2(H1) and linf(L2) norms for an implicit Euler discretization in time. We give numerical illustrations to highlight the performances of phi-FEM, which combines optimal convergence accuracy, easy implementation process and fastness.