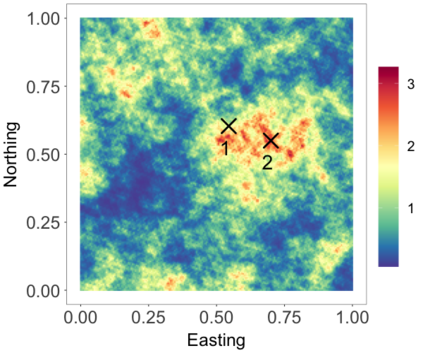
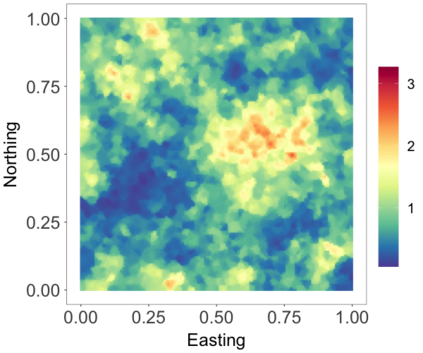
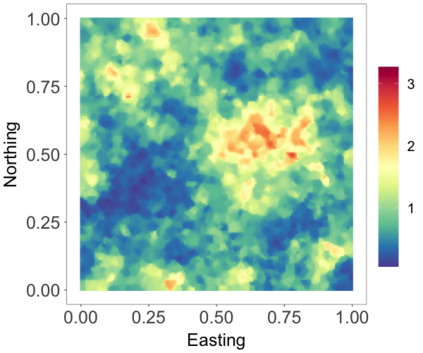
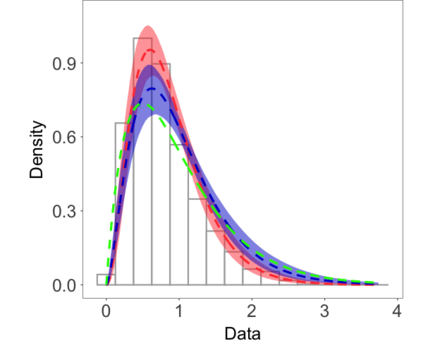
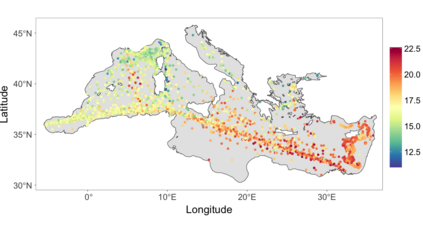
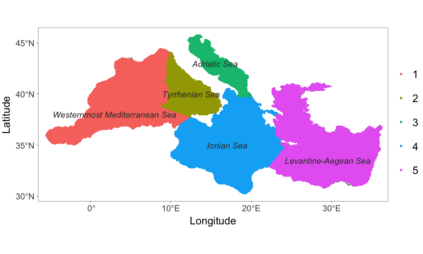
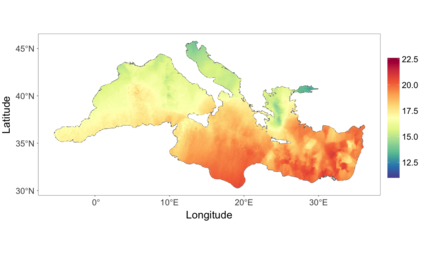
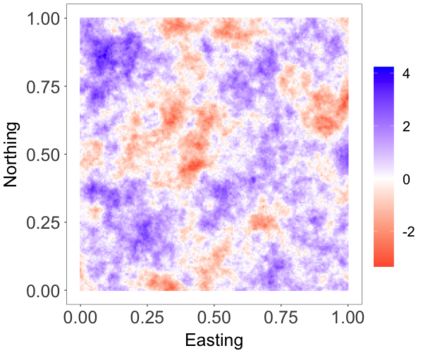
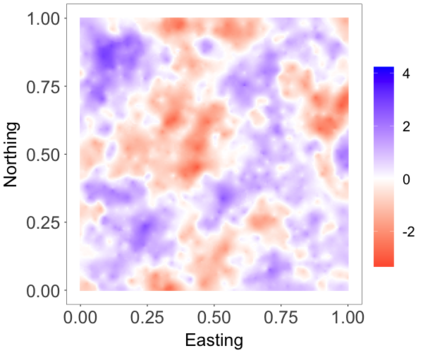
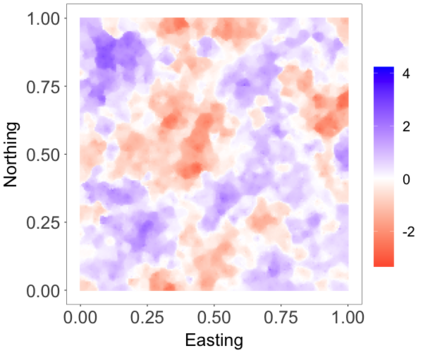
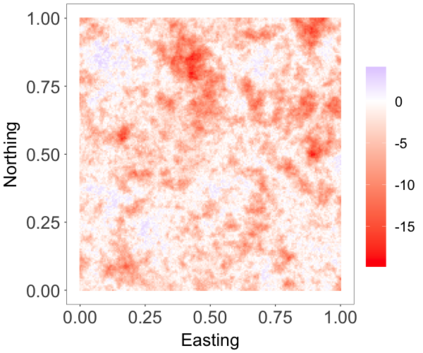
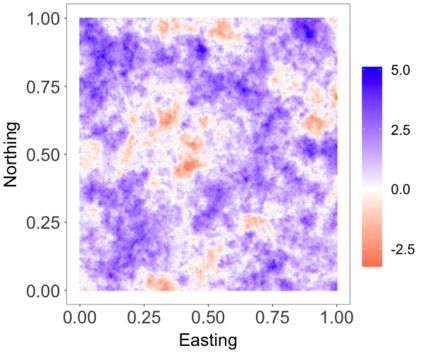
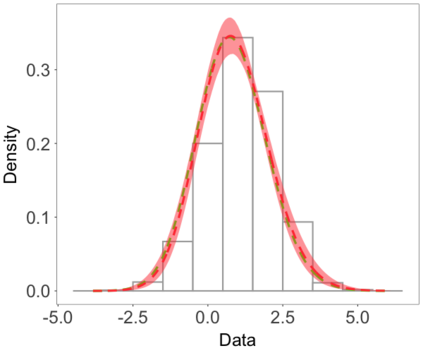
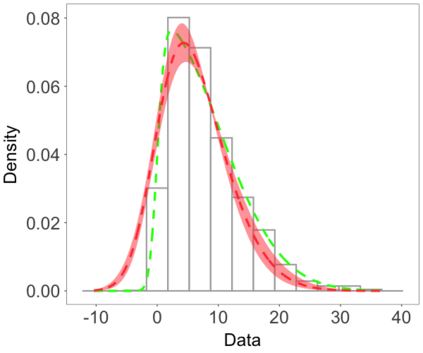
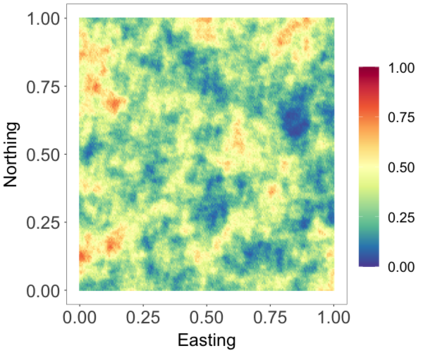
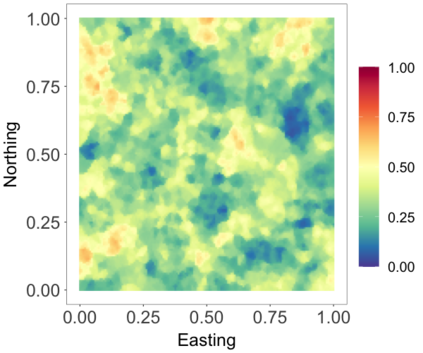
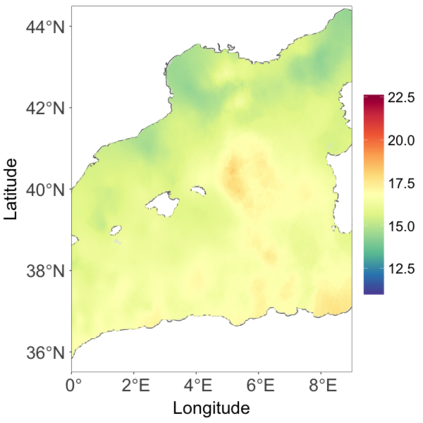
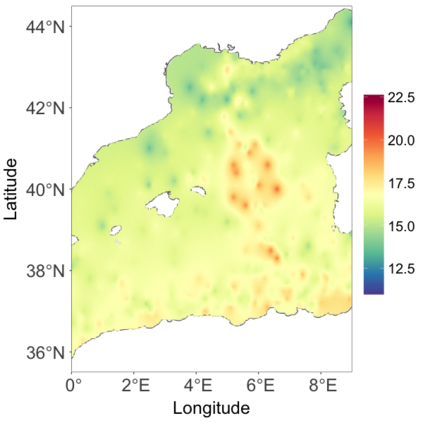
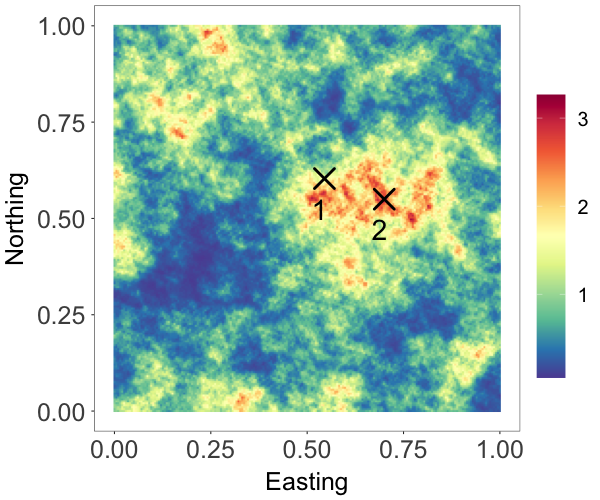
We develop a class of nearest-neighbor mixture models that provide direct, computationally efficient, probabilistic modeling for non-Gaussian geospatial data. The class is defined over a directed acyclic graph, which implies conditional independence in representing a multivariate distribution through factorization into a product of univariate conditionals, and is extended to a full spatial process. We model each conditional as a mixture of spatially varying transition kernels, with locally adaptive weights, for each one of a given number of nearest neighbors. The modeling framework emphasizes the description of non-Gaussian dependence at the data level, in contrast with approaches that introduce a spatial process for transformed data, or for functionals of the data probability distribution. Thus, it facilitates efficient, full simulation-based inference. We study model construction and properties analytically through specification of bivariate distributions that define the local transition kernels, providing a general strategy for modeling general types of non-Gaussian data. Regarding computation, the framework lays out a new approach to handling spatial data sets, leveraging a mixture model structure to avoid computational issues that arise from large matrix operations. We illustrate the methodology using synthetic data examples and an analysis of Mediterranean Sea surface temperature observations.
翻译:我们开发了近邻混合模型的类别,为非古裔地理空间数据提供直接、计算高效、概率模型,该类由定向环状图确定,这意味着通过将因数分解成单体条件的产物来代表多变量分布的有条件独立性,扩展至完整的空间过程。我们将每种模型都作为空间上差异的过渡内核的混合体,并带有当地适应权重,为每个特定数量的近邻提供。模型框架强调在数据一级说明非古裔依赖性,而采用的方法则为转换的数据或数据概率分布功能引入空间过程。因此,它有利于高效、全面的模拟推论。我们通过确定本地转型内核的双轨分布法来研究模型的构建和属性,为非古裔数据的一般类型建模提供了一种总体战略。在计算方面,该框架提出了处理空间数据集的新办法,利用混合模型结构来利用数据转换数据转换,或数据概率分布的功能。因此,我们通过分析双轨法来研究模型的构建模型和属性,从而避免从大型的海面分析方法中产生。