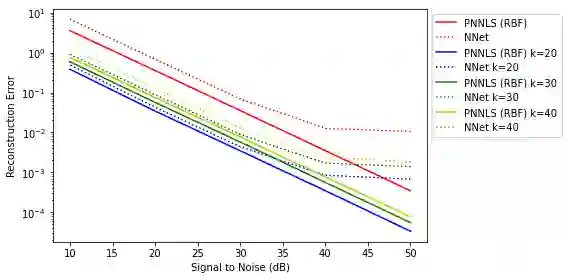
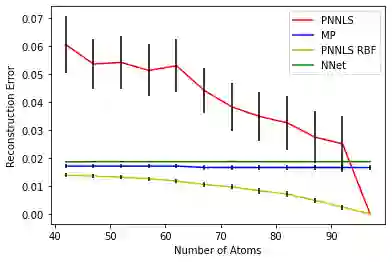
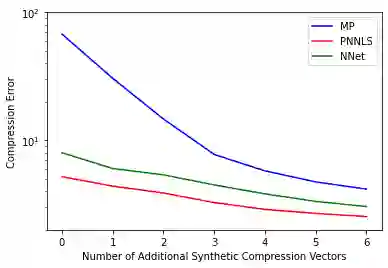
Hyperspectral measurements from long range sensors can give a detailed picture of the items, materials, and chemicals in a scene but analysis can be difficult, slow, and expensive due to high spatial and spectral resolutions of state-of-the-art sensors. As such, sparsity is important to enable the future of spectral compression and analytics. It has been observed that environmental and atmospheric effects, including scattering, can produce nonlinear effects posing challenges for existing source separation and compression methods. We present a novel transformation into Hilbert spaces for pruning and constructing sparse representations via non-negative least squares minimization. Then we introduce max likelihood compression vectors to decrease information loss. Our approach is benchmarked against standard pruning and least squares as well as deep learning methods. Our methods are evaluated in terms of overall spectral reconstruction error and compression rate using real and synthetic data. We find that pruning least squares methods converge quickly unlike matching pursuit methods. We find that Hilbert space pruning can reduce error by as much as 40% of the error of standard pruning and also outperform neural network autoencoders.
翻译:暂无翻译