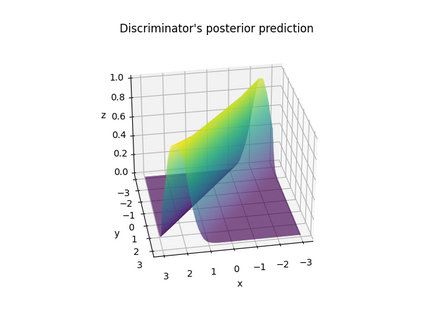
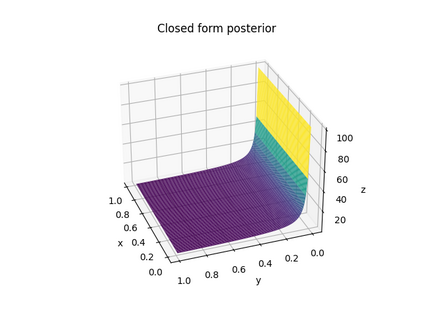
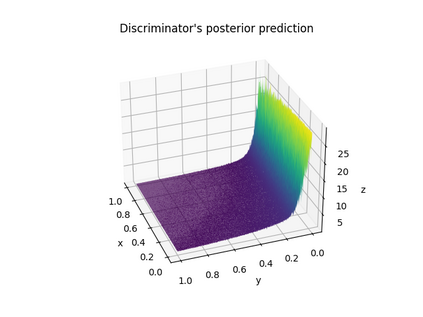
In deep learning, classification tasks are formalized as optimization problems solved via the minimization of the cross-entropy. However, recent advancements in the design of objective functions allow the $f$-divergence measure to generalize the formulation of the optimization problem for classification. With this goal in mind, we adopt a Bayesian perspective and formulate the classification task as a maximum a posteriori probability problem. We propose a class of objective functions based on the variational representation of the $f$-divergence, from which we extract a list of five posterior probability estimators leveraging well-known $f$-divergences. In addition, driven by the challenge of improving the state-of-the-art approach, we propose a bottom-up method that leads us to the formulation of a new objective function (and posterior probability estimator) corresponding to a novel $f$-divergence referred to as shifted log (SL). First, we theoretically prove the convergence property of the posterior probability estimators. Then, we numerically test the set of proposed objective functions in three application scenarios: toy examples, image data sets, and signal detection/decoding problems. The analyzed tasks demonstrate the effectiveness of the proposed estimators and that the SL divergence achieves the highest classification accuracy in almost all the scenarios.
翻译:暂无翻译