Stochastic Transport with Lévy Noise -- Fully Discrete Numerical Approximation

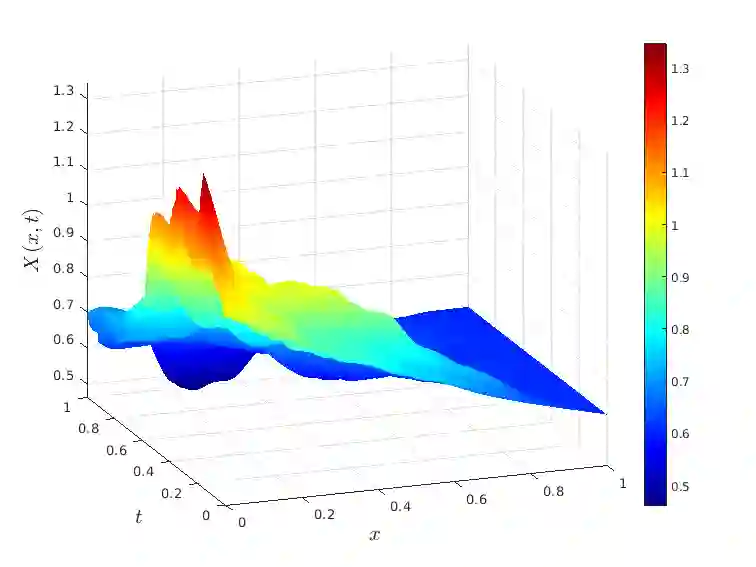
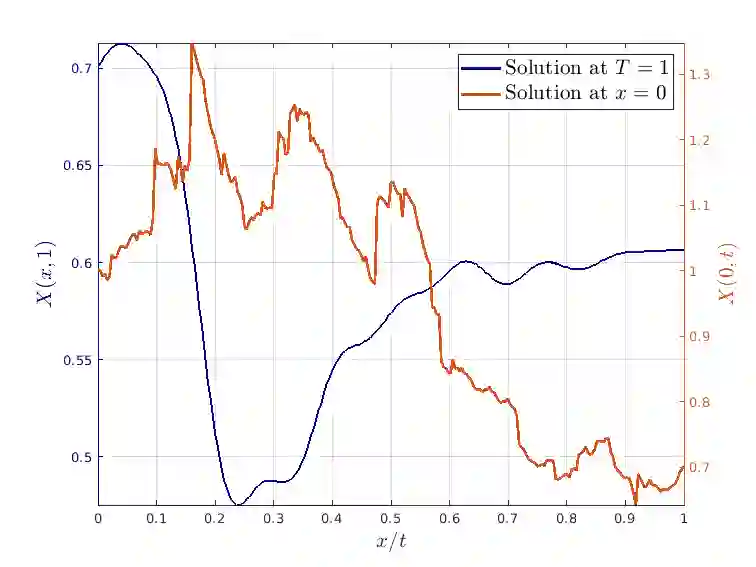
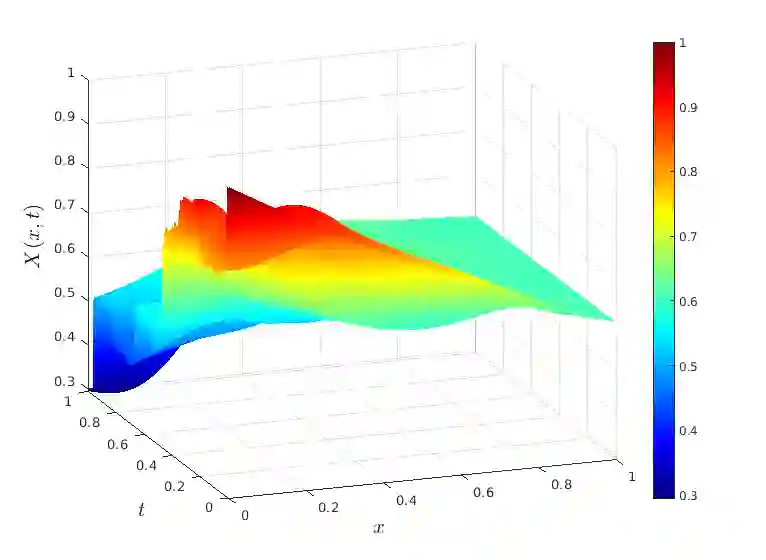
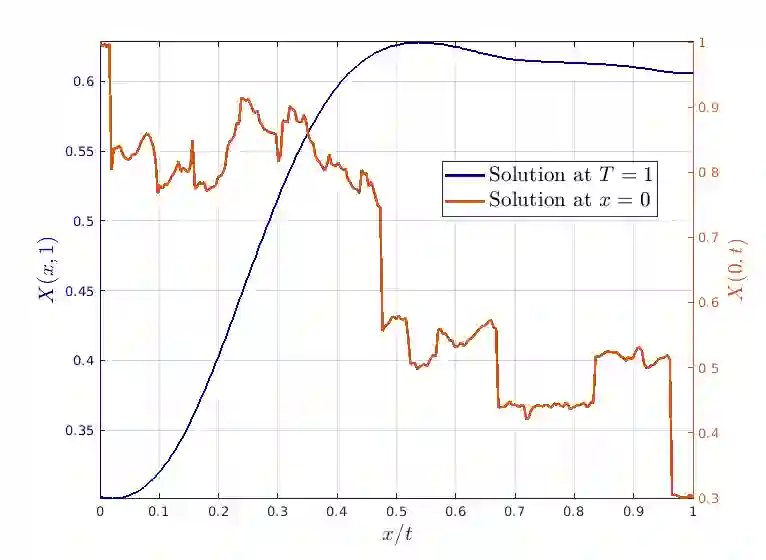
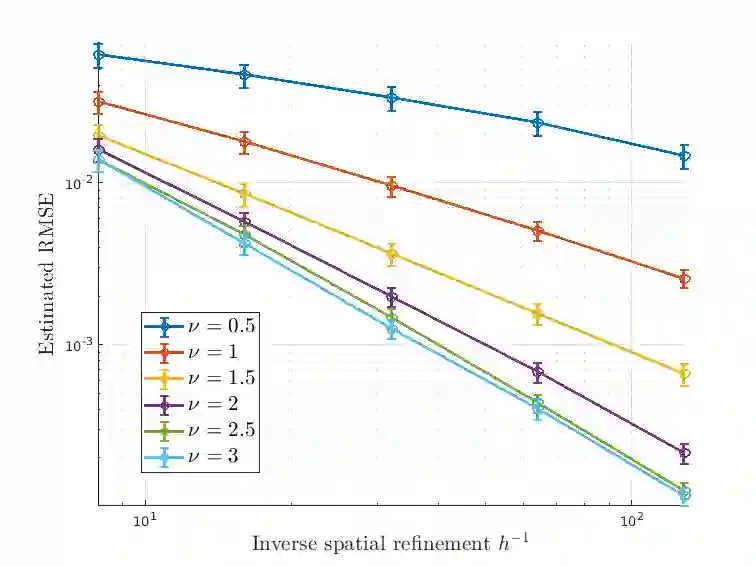
Semilinear hyperbolic stochastic partial differential equations (SPDEs) find widespread applications in the natural and engineering sciences. However, the traditional Gaussian setting may prove too restrictive, as phenomena in mathematical finance, porous media, and pollution models often exhibit noise of a different nature. To capture temporal discontinuities and accommodate heavy-tailed distributions, Hilbert space-valued L\'evy processes or L\'evy fields are employed as driving noise terms. The numerical discretization of such SPDEs presents several challenges. The low regularity of the solution in space and time leads to slow convergence rates and instability in space/time discretization schemes. Furthermore, the L\'evy process can take values in an infinite-dimensional Hilbert space, necessitating projections onto finite-dimensional subspaces at each discrete time point. Additionally, unbiased sampling from the resulting L\'evy field may not be feasible. In this study, we introduce a novel fully discrete approximation scheme that tackles these difficulties. Our main contribution is a discontinuous Galerkin scheme for spatial approximation, derived naturally from the weak formulation of the SPDE. We establish optimal convergence properties for this approach and combine it with a suitable time stepping scheme to prevent numerical oscillations. Furthermore, we approximate the driving noise process using truncated Karhunen-Lo\`eve expansions. This approximation yields a sum of scaled and uncorrelated one-dimensional L\'evy processes, which can be simulated with controlled bias using Fourier inversion techniques.