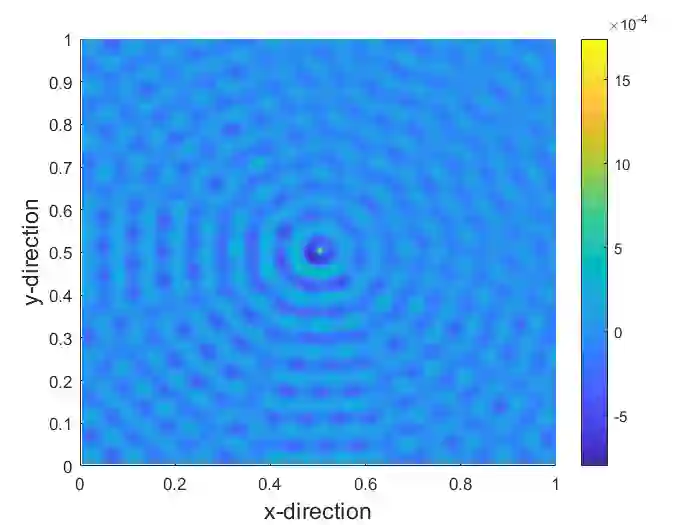
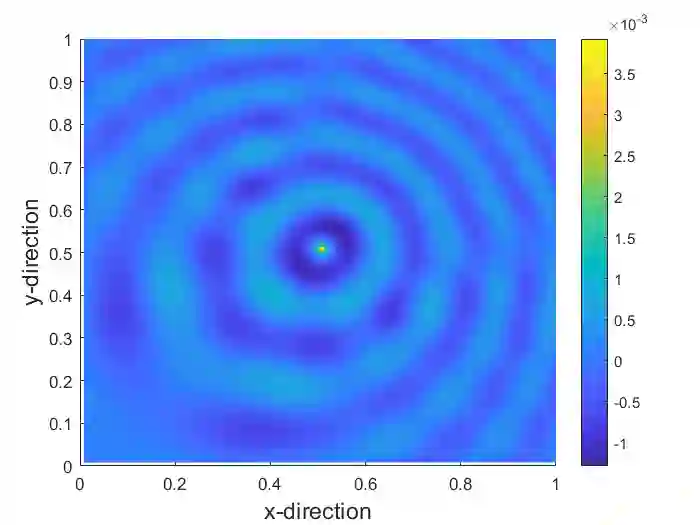
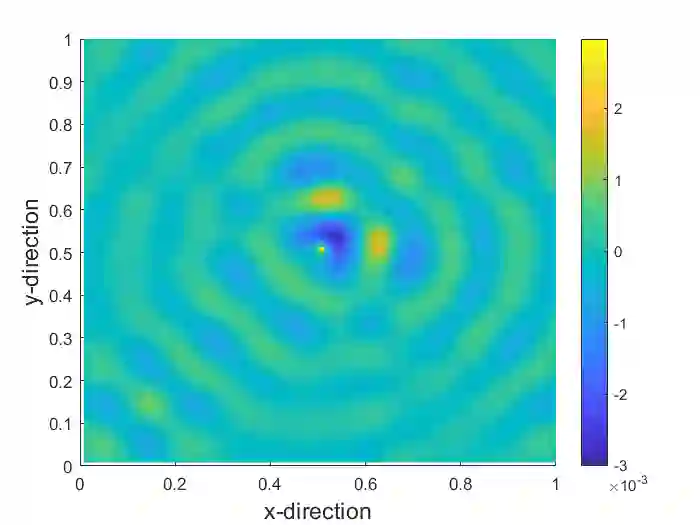
Getting standard multigrid to work efficiently for the high-frequency Helmholtz equation has been an open problem in applied mathematics for years. Much effort has been dedicated to finding solution methods which can use multigrid components to obtain solvers with a linear time complexity. In this work we present one among the first stand-alone multigrid solvers for the 2D Helmholtz equation using both a constant and non-constant wavenumber model problem. We use standard smoothing techniques and do not impose any restrictions on the number of grid points per wavelength on the coarse-grid. As a result we are able to obtain a full V- and W-cycle algorithm. The key features of the algorithm are the use of higher-order inter-grid transfer operators combined with a complex constant in the coarsening process. Using weighted-Jacobi smoothing, we obtain a solver which is $h-$independent and scales linearly with the wavenumber $k$. Numerical results using 1 to 5 GMRES(3) smoothing steps approach $k-$ and $h-$ independent convergence, when combined with the higher-order inter-grid transfer operators and a small or even zero complex shift. The proposed algorithm provides an important step towards the perpetuating branch of research in finding scalable solvers for challenging wave propagation problems.
翻译:暂无翻译