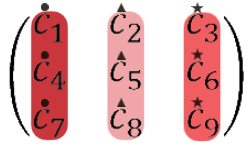
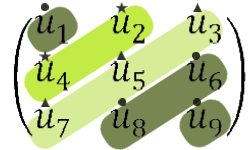
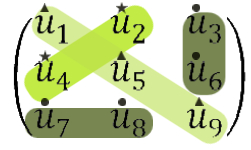
We consider the problem of allocating indivisible goods to agents with additive valuation functions. Kurokawa, Procaccia and Wang {[JACM, 2018]} present instances for which every allocation gives some agent less than her maximin share. We present such examples with larger gaps. For three agents and nine items, we design an instance in which at least one agent does not get more than a $\frac{39}{40}$ fraction of her maximin share. {Moreover, we show that there is no negative example in which the difference between the number of items and the number of agents is smaller than six, and that the gap (of $\frac{1}{40}$) of our example is worst possible among all instances with nine items.} For $n \ge 4$ agents, we show examples in which at least one agent does not get more than a $1 - \frac{1}{n^4}$ fraction of her maximin share. {In the instances designed by Kurokawa, Procaccia and Wang, the gap is exponentially small in $n$.} Our proof techniques extend to allocation of chores (items of negative value), though the quantitative bounds for chores are different from those for goods. For three agents and nine chores, we design an instance in which the MMS gap is $\frac{1}{43}$.
翻译:我们考虑的是将不可分割的货物分配给具有添加性估价功能的代理商的问题。 木川、 Procaccia 和 Wang {[JACM, 2018]} 目前的事例中,每项分配给某些代理商的分量低于其最大份额的分量。 我们展示了这样的例子:对于三个代理商和九个项目,我们设计了一个至少一个代理商的分量不超过其最大份额的1美元(frac{39 ⁇ 40})。 {此外,我们显示,不存在一个负面的例子,表明物品数量与代理商数量之间的差别小于6个,而我们的例子($frac{1 ⁇ 40})中的差($frac{1 ⁇ 40美元)在九个项目中都可能最差。} 关于4美元代理商,我们设计了一个至少一个代理商的分量不超过1美元(frac}1 ⁇ n ⁇ 4}其最大份额的分量的分量。 {我们展示的是, {在由Kurokawa、 Procaccicacacaa 和 Wang 设计的情况中, 差距是指数小于1美元。 。 。} 我们的三件中, 我们的代理商的理商的分量的分量的分量是3个。