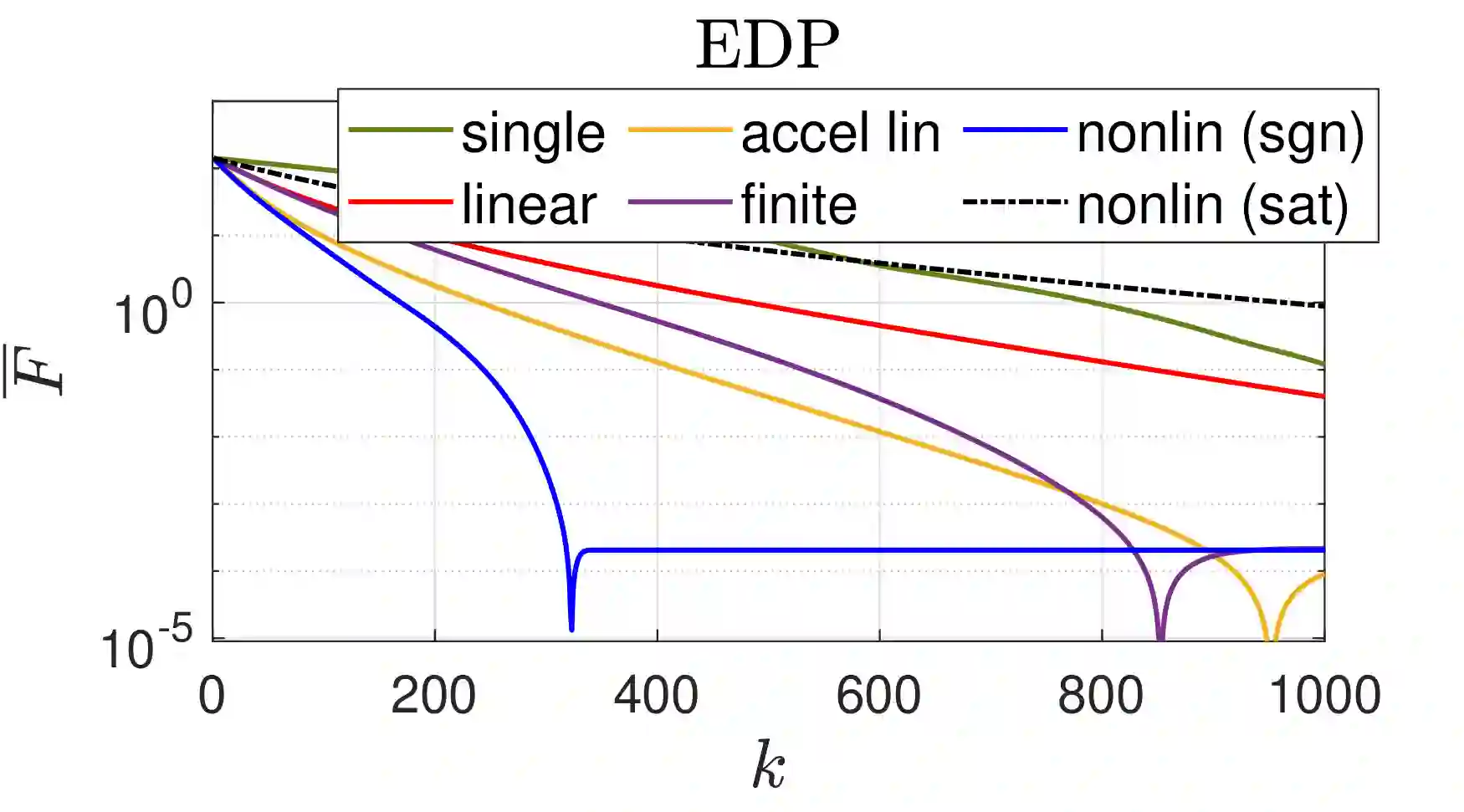
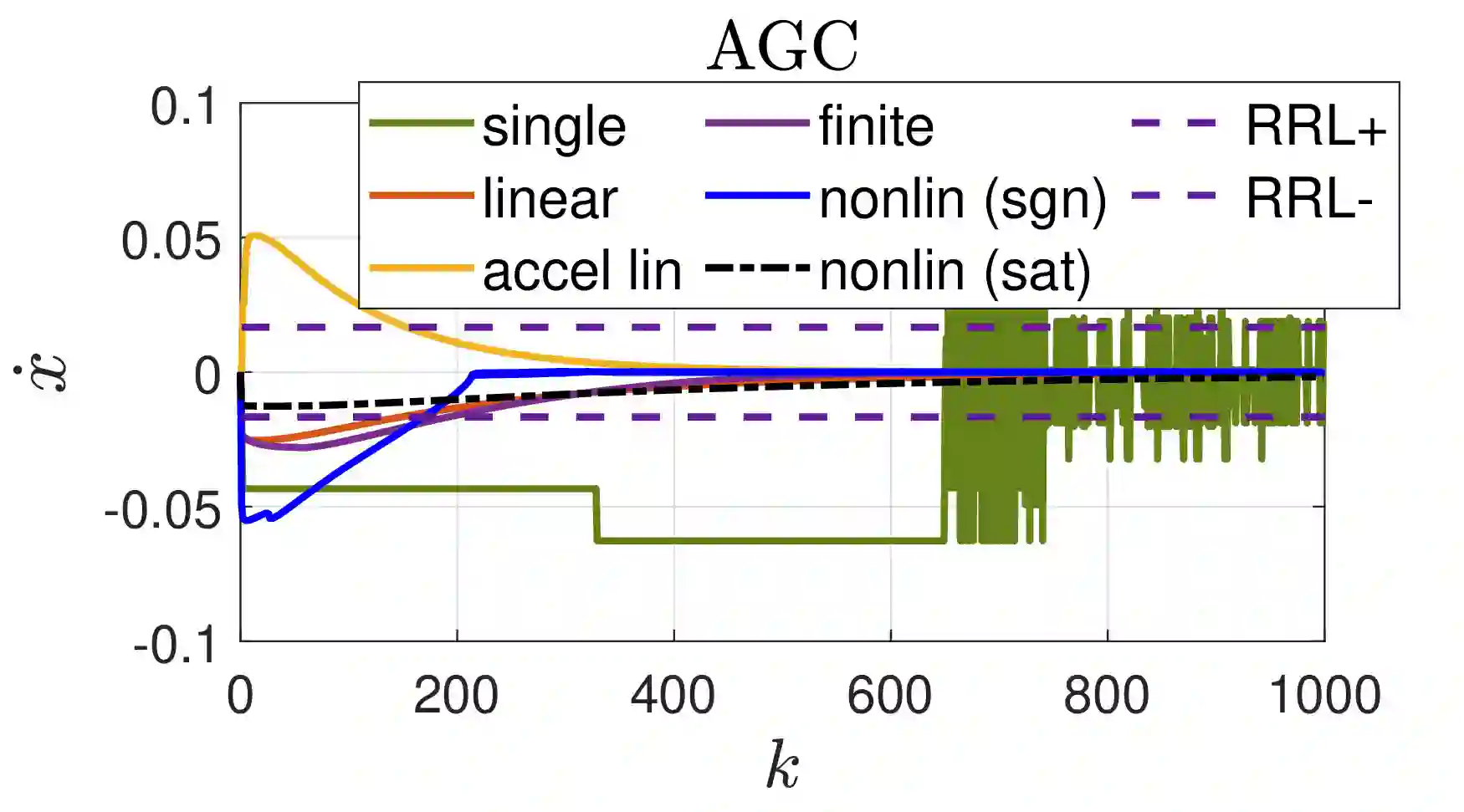
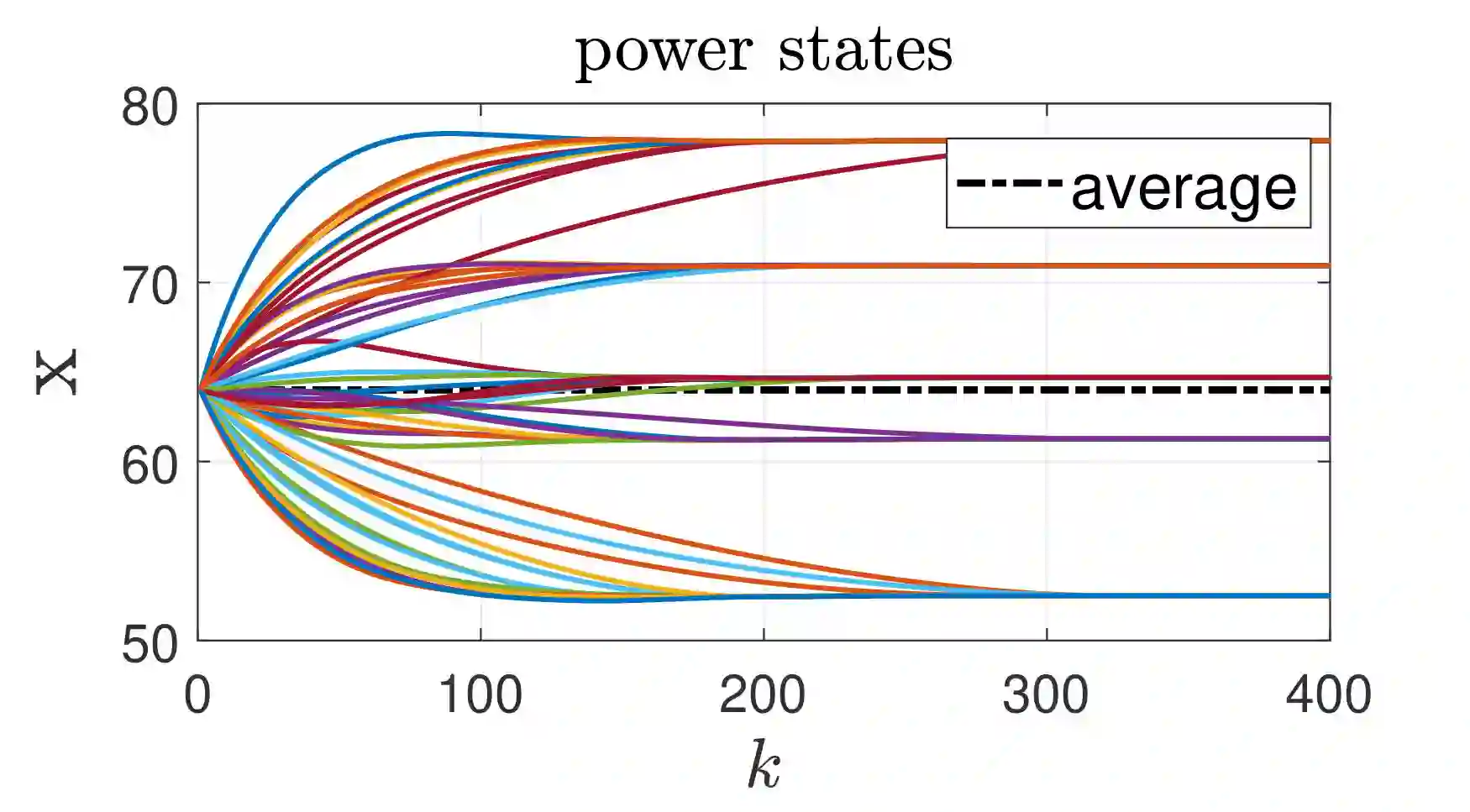
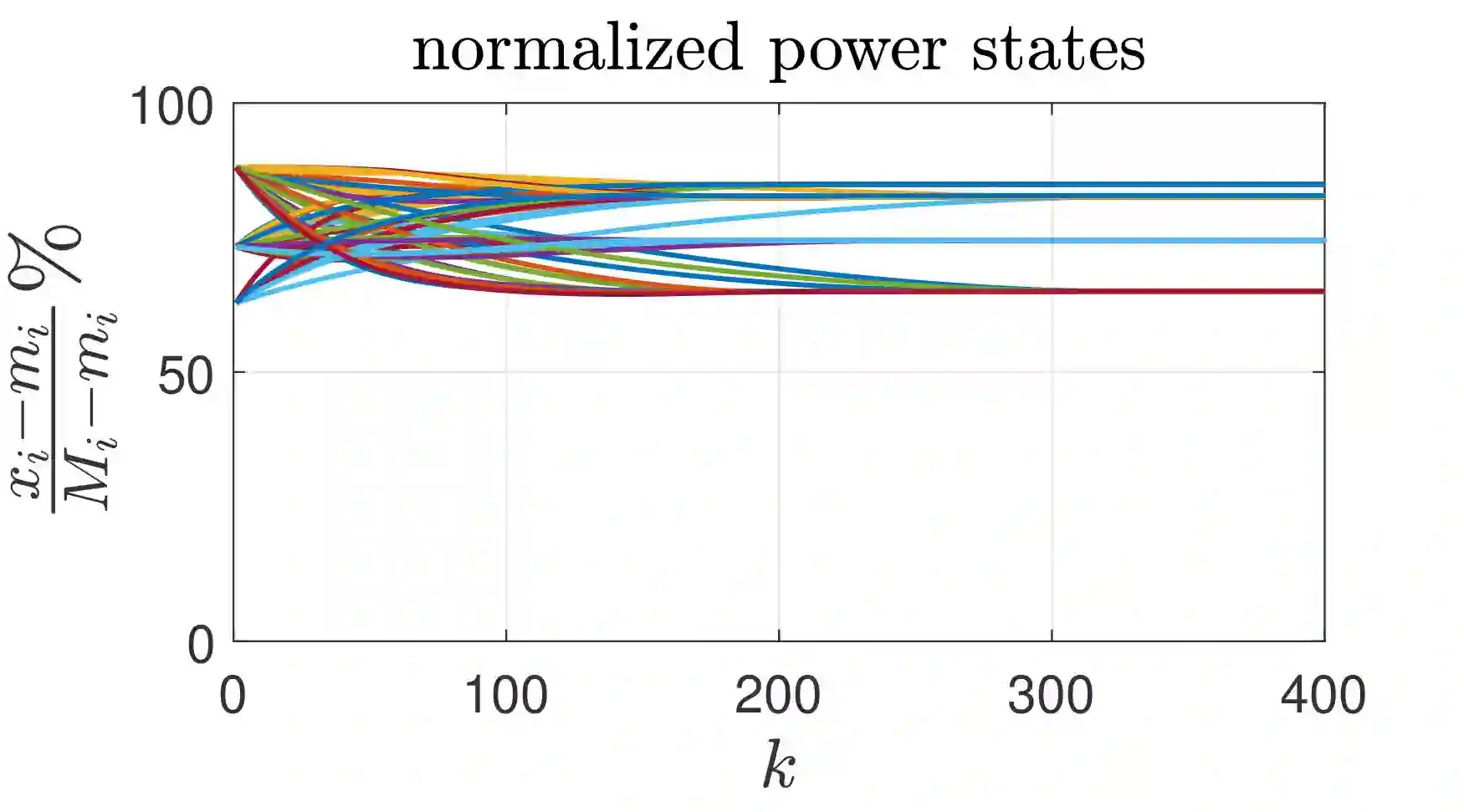
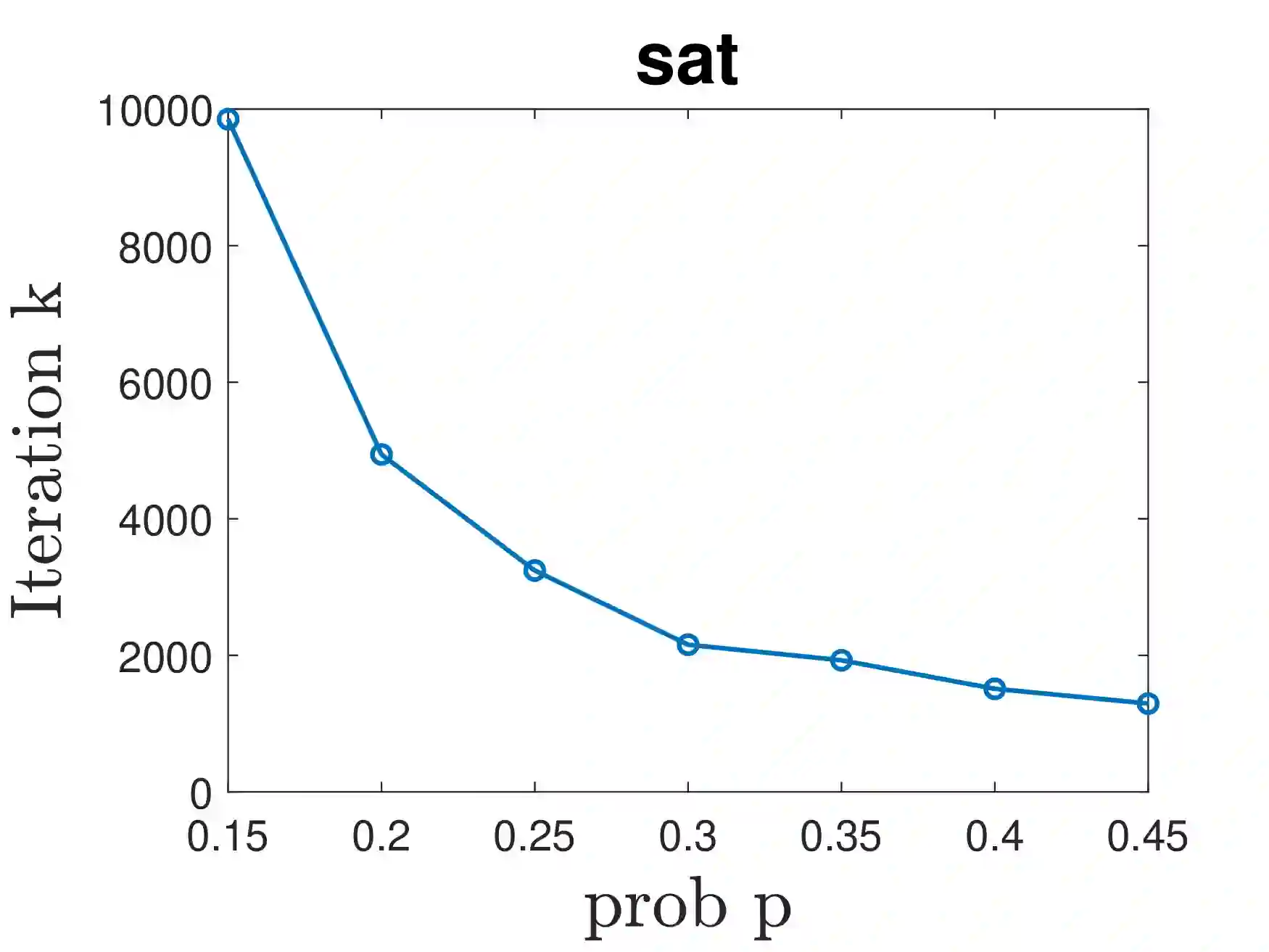
This paper proposes two nonlinear dynamics to solve constrained distributed optimization problem for resource allocation over a multi-agent network. In this setup, coupling constraint refers to resource-demand balance which is preserved at all-times. The proposed solutions can address various model nonlinearities, for example, due to quantization and/or saturation. Further, it allows to reach faster convergence or to robustify the solution against impulsive noise or uncertainties. We prove convergence over weakly connected networks using convex analysis and Lyapunov theory. Our findings show that convergence can be reached for general sign-preserving odd nonlinearity. We further propose delay-tolerant mechanisms to handle general bounded heterogeneous time-varying delays over the communication network of agents while preserving all-time feasibility. This work finds application in CPU scheduling and coverage control among others. This paper advances the state-of-the-art by addressing (i) possible nonlinearity on the agents/links, meanwhile handling (ii) resource-demand feasibility at all times, (iii) uniform-connectivity instead of all-time connectivity, and (iv) possible heterogeneous and time-varying delays. To our best knowledge, no existing work addresses contributions (i)-(iv) altogether. Simulations and comparative analysis are provided to corroborate our contributions.
翻译:暂无翻译