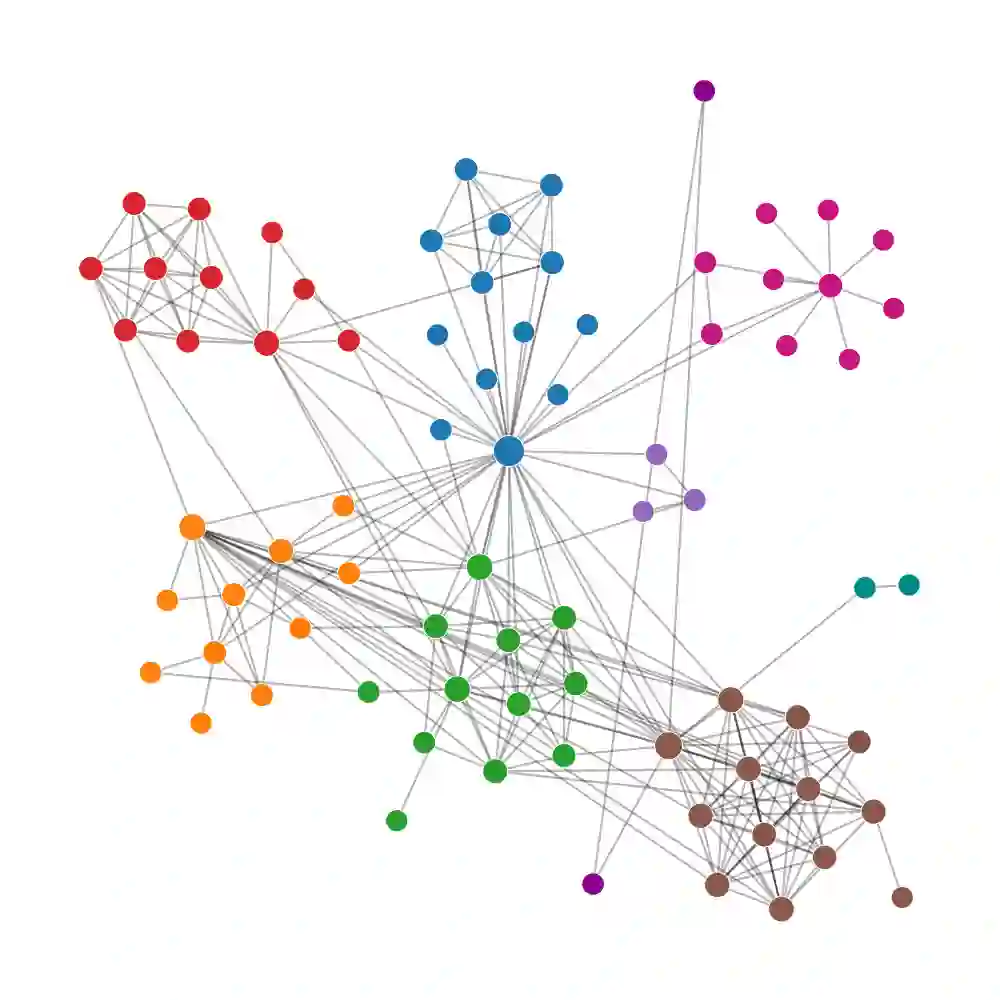
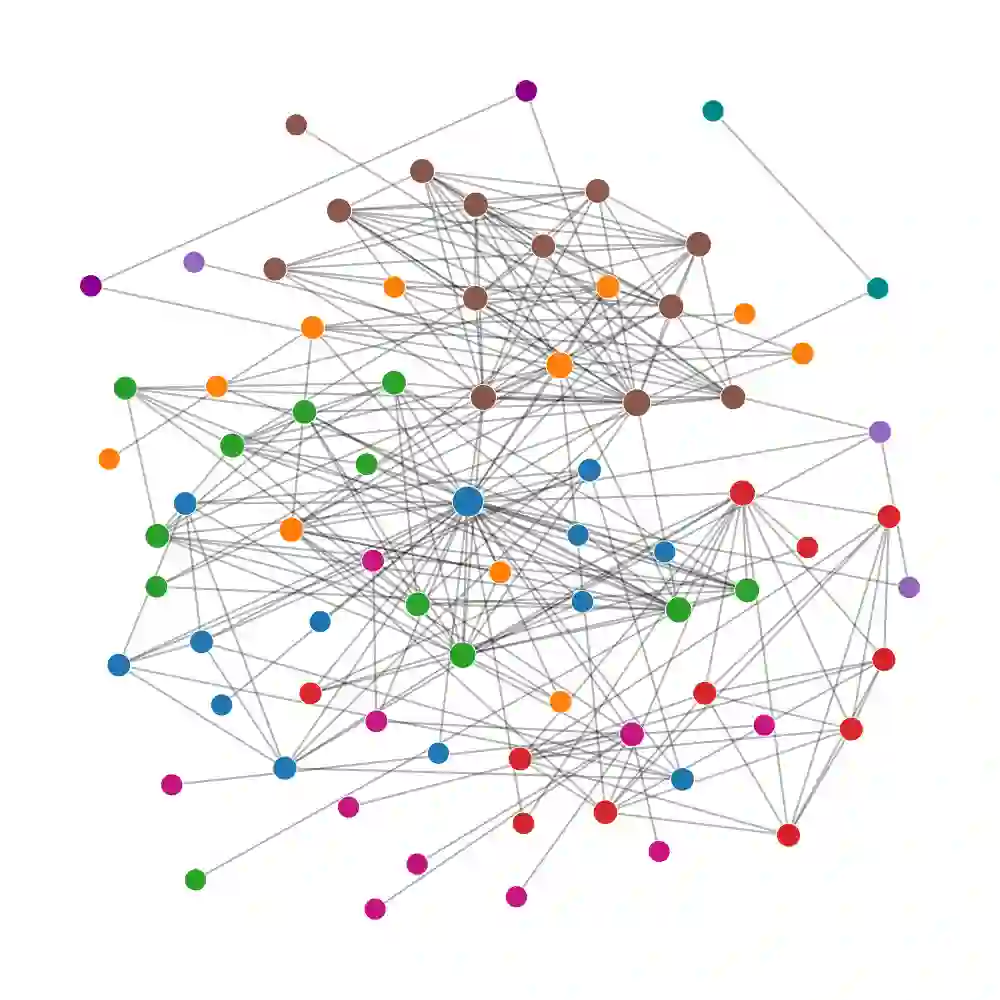
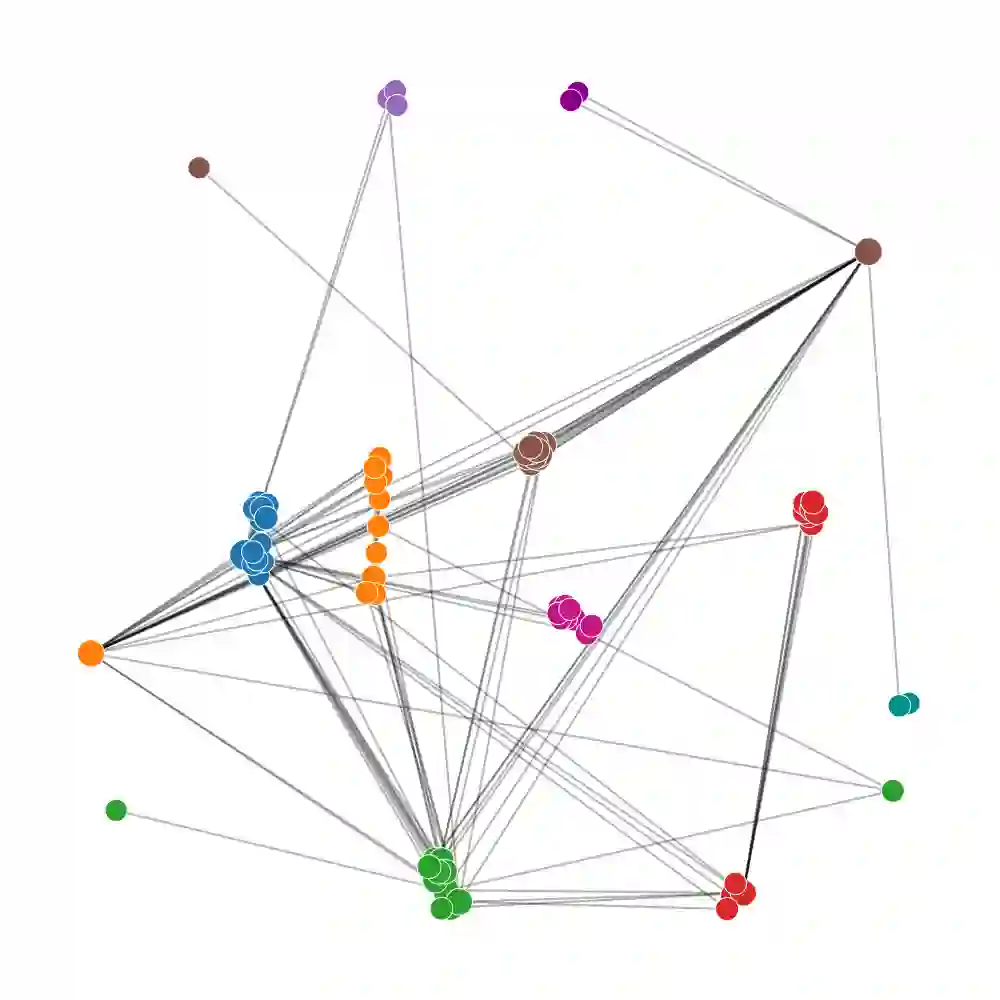
Node-link diagrams are widely used to visualize graphs. Most graph layout algorithms only use graph topology for aesthetic goals (e.g., minimize node occlusions and edge crossings) or use node attributes for exploration goals (e.g., preserve visible communities). Existing hybrid methods that bind the two perspectives still suffer from various generation restrictions (e.g., limited input types and required manual adjustments and prior knowledge of graphs) and the imbalance between aesthetic and exploration goals. In this paper, we propose a flexible embedding-based graph exploration pipeline to enjoy the best of both graph topology and node attributes. First, we leverage embedding algorithms for attributed graphs to encode the two perspectives into latent space. Then, we present an embedding-driven graph layout algorithm, GEGraph, which can achieve aesthetic layouts with better community preservation to support an easy interpretation of the graph structure. Next, graph explorations are extended based on the generated graph layout and insights extracted from the embedding vectors. Illustrated with examples, we build a layout-preserving aggregation method with Focus+Context interaction and a related nodes searching approach with multiple proximity strategies. Finally, we conduct quantitative and qualitative evaluations, a user study, and two case studies to validate our approach.
翻译:节点链接图表被广泛用于图形的可视化。 多数图表布局算法仅使用图形表层, 用于美学目标( 例如, 最小化节点隔离和边缘交叉点), 或用于勘探目标( 比如, 保存可见社区 ) 。 连接两种观点的现有混合方法仍然受到不同的生成限制( 例如, 有限的输入类型和所需的手工调整以及先前对图表的了解) 以及美学和勘探目标之间的不平衡。 本文中, 我们提议灵活嵌入基于图形的图表勘探管道, 以享受最佳的图形表层和节点属性。 首先, 我们利用可归属的图形嵌入算法将两种观点编码到潜在空间。 然后, 我们展示了嵌入驱动的图形布局算法, GEGraph, 它可以实现美学布局, 支持对图形结构的简单解释。 下一步, 图形勘探是根据生成的图形布局和从嵌入矢量矢量中提取的洞察结果扩展的。 Illusted with 示例, 我们构建了一种保留配置的配置组方法, 与Focus+Context 对比和相关的定性方法, 搜索。 最后, 我们用两种选择了一种用户对立项的比较和定性方法。