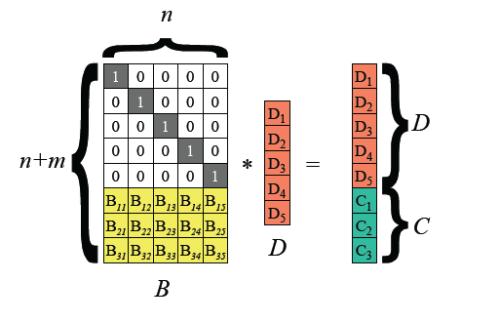
Distributed matrix computations over large clusters can suffer from the problem of slow or failed worker nodes (called stragglers) which can dominate the overall job execution time. Coded computation utilizes concepts from erasure coding to mitigate the effect of stragglers by running 'coded' copies of tasks comprising a job; stragglers are typically treated as erasures. While this is useful, there are issues with applying, e.g., MDS codes in a straightforward manner. Several practical matrix computation scenarios involve sparse matrices. MDS codes typically require dense linear combinations of submatrices of the original matrices which destroy their inherent sparsity. This is problematic as it results in significantly higher worker computation times. Moreover, treating slow nodes as erasures ignores the potentially useful partial computations performed by them. Furthermore, some MDS techniques also suffer from significant numerical stability issues. In this work we present schemes that allow us to leverage partial computation by stragglers while imposing constraints on the level of coding that is required in generating the encoded submatrices. This significantly reduces the worker computation time as compared to previous approaches and results in improved numerical stability in the decoding process. Exhaustive numerical experiments on Amazon Web Services (AWS) clusters support our findings.
翻译:在大型组群中,分布式矩阵的计算可能会受到慢速或失败的工人节点(所谓的分流器)问题的影响,这可以在整个工作执行时间中占主导地位。 代码计算使用从删除编码编码的概念,通过运行由工作构成的“ 编码” 任务副本来减轻分解器的影响; 通常将分流器作为消化器处理。 虽然这是有用的,但有一些应用问题,例如MDS 代码, 有一些实际的矩阵计算方案涉及稀释矩阵。 MDS 代码通常需要将原始矩阵的子矩阵进行密集线性组合,这些子矩阵摧毁了它们固有的宽度。 这样做有问题, 因为它导致工人计算时间的大幅提高。 此外, 将慢节点视为删除时忽略了由它们完成的可能有用的部分计算; 此外, 一些MDS 技术也存在重大的数字稳定性问题。 在这项工作中,我们提出的计划允许我们利用分流器进行部分计算, 而对生成编码子矩阵所需的编码的分母体水平施加限制。 这大大降低了工人计算时间, 因为它导致工人计算结果在先前的亚流体实验中, 这大大缩短了工人计算过程, 相对于亚流体实验中SARSA 。