Hausdorff Distance between Norm Balls and their Linear Maps

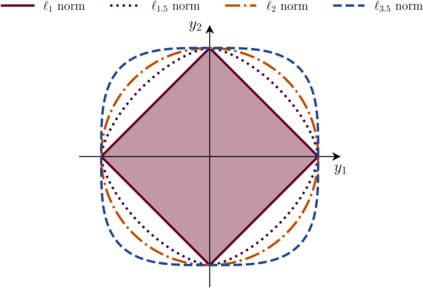
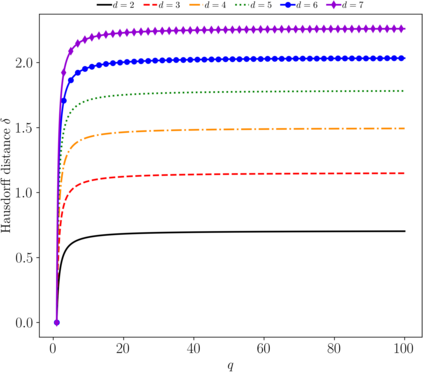
We consider the problem of computing the (two-sided) Hausdorff distance between the unit $\ell_{p_{1}}$ and $\ell_{p_{2}}$ norm balls in finite dimensional Euclidean space for $1 < p_1 < p_2 \leq \infty$, and derive a closed-form formula for the same. We also derive a closed-form formula for the Hausdorff distance between the $k_1$ and $k_2$ unit $D$-norm balls, which are certain polyhedral norm balls in $d$ dimensions for $1 \leq k_1 < k_2 \leq d$. When two different $\ell_p$ norm balls are transformed via a common linear map, we obtain several estimates for the Hausdorff distance between the resulting convex sets. These estimates upper bound the Hausdorff distance or its expectation, depending on whether the linear map is arbitrary or random. We then generalize the developments for the Hausdorff distance between two set-valued integrals obtained by applying a parametric family of linear maps to different $\ell_p$ unit norm balls, and then taking the Minkowski sums of the resulting sets in a limiting sense. To illustrate an application, we show that the problem of computing the Hausdorff distance between the reach sets of a linear dynamical system with different unit norm ball-valued input uncertainties, reduces to this set-valued integral setting.