Rectangular Flows for Manifold Learning

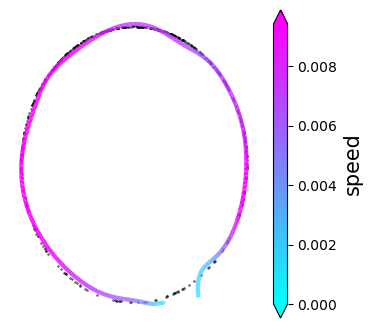
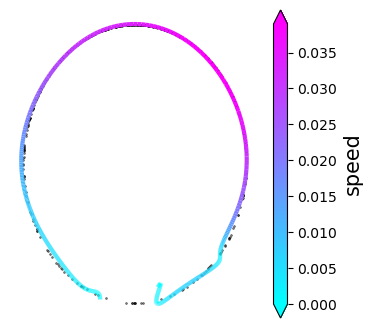
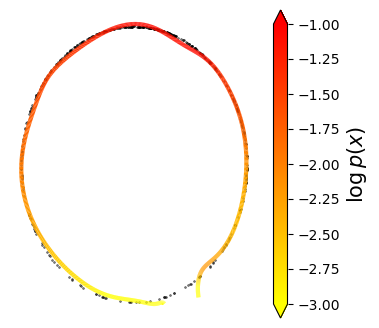
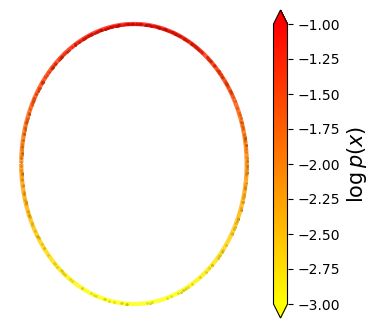
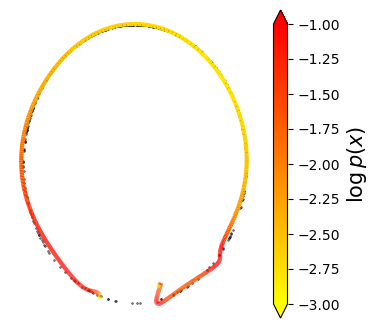
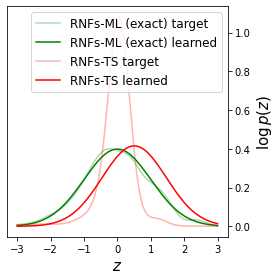
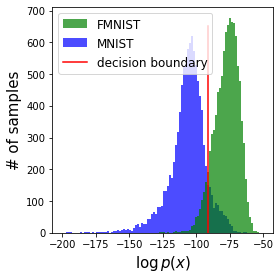
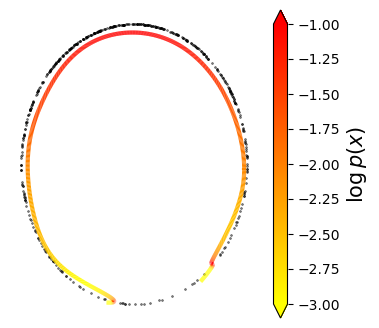
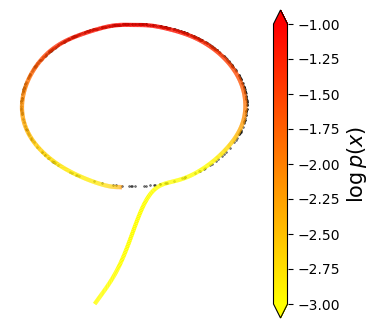
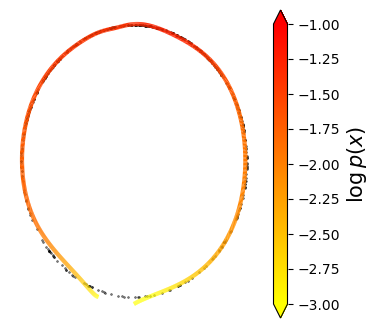
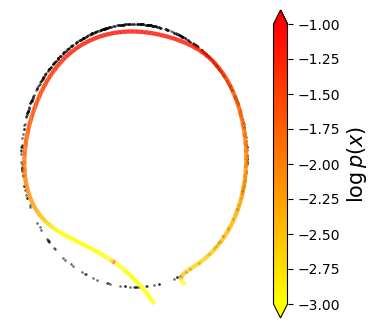
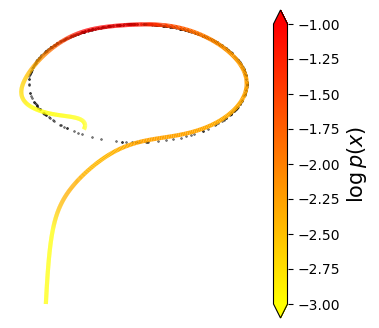
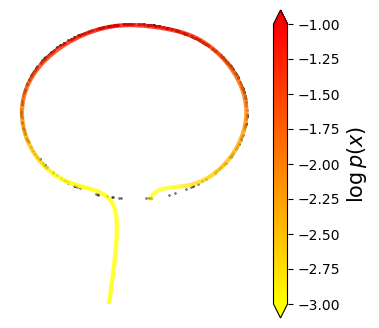
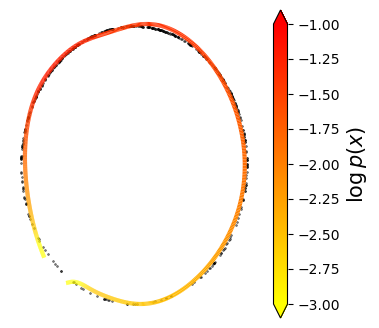
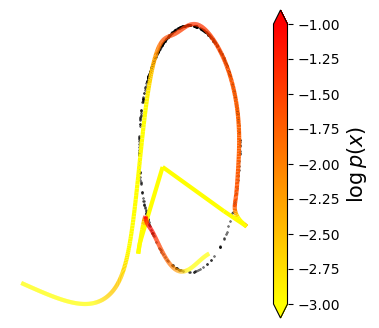
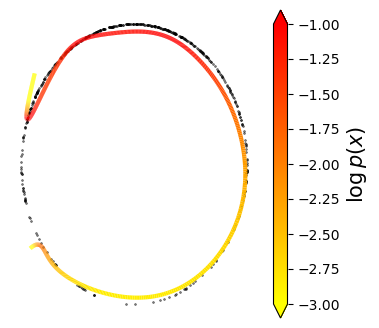
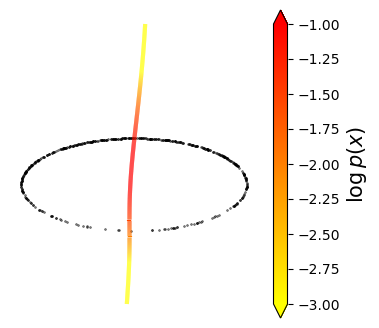
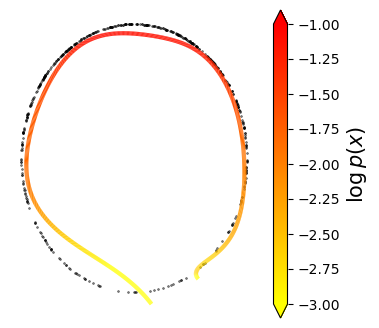
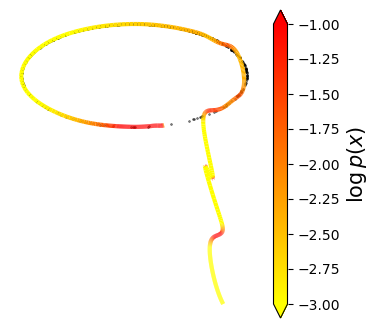
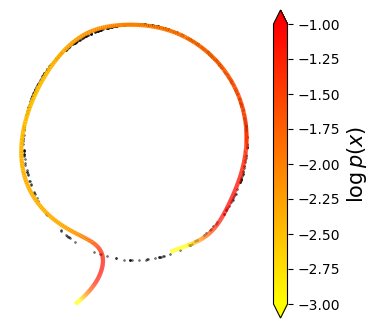
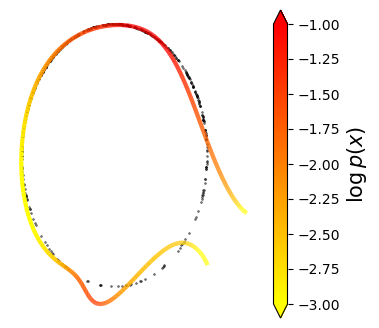
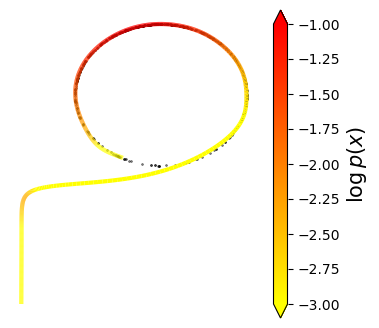
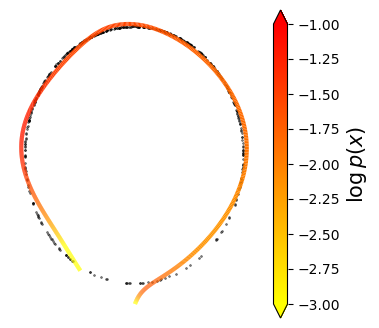
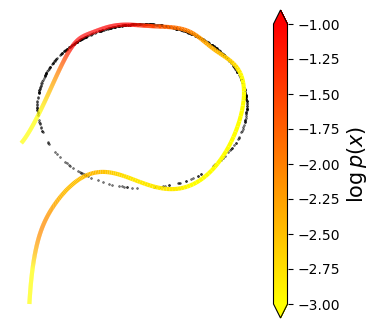
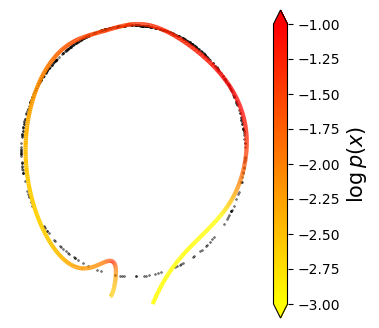
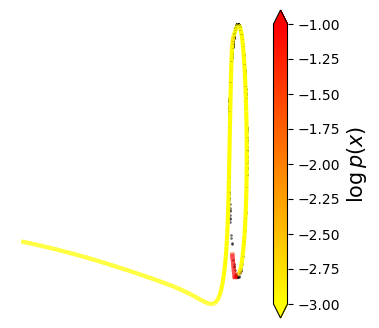
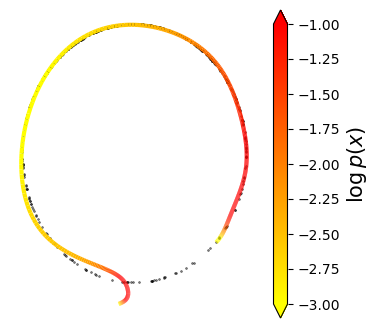
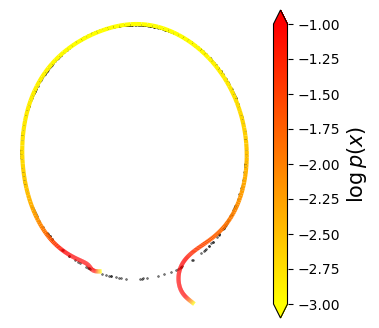
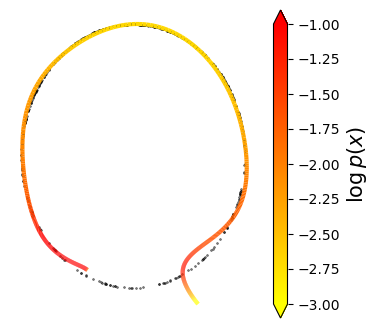
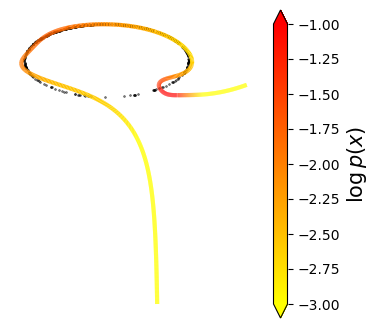
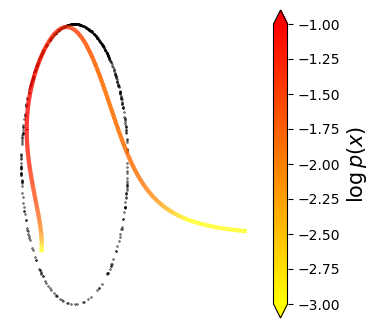
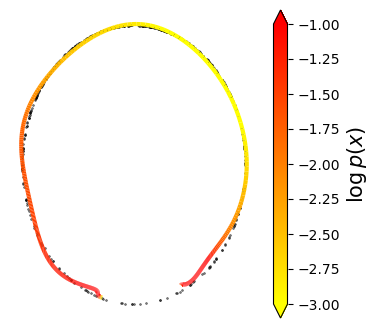
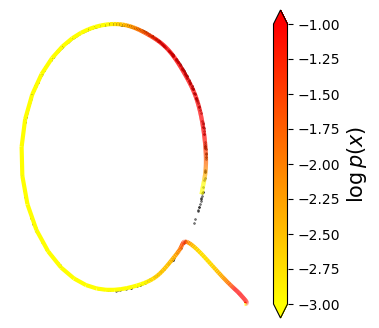
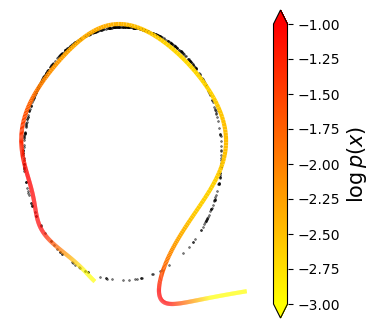
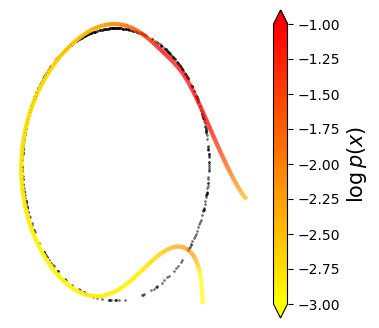
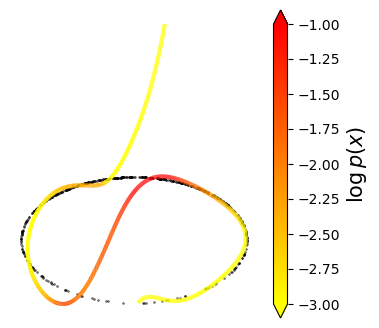
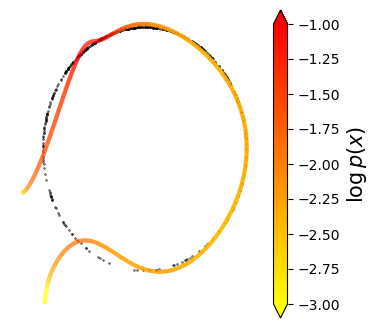
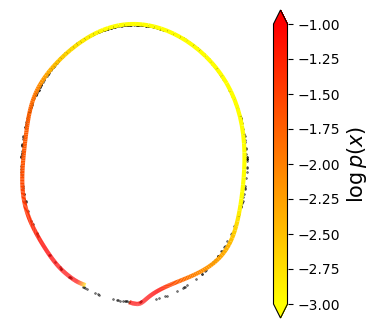
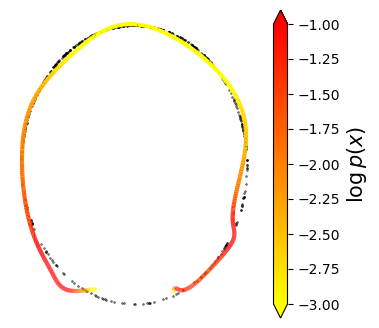
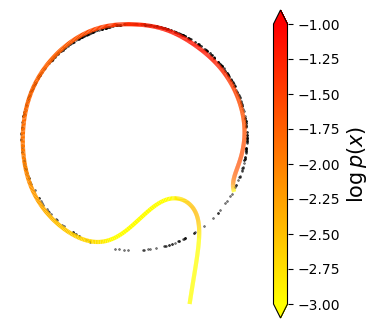
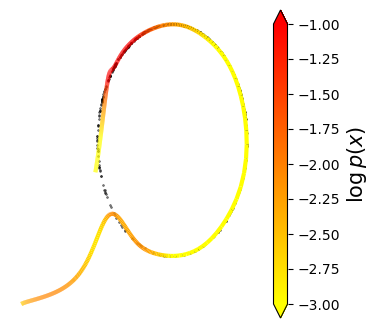
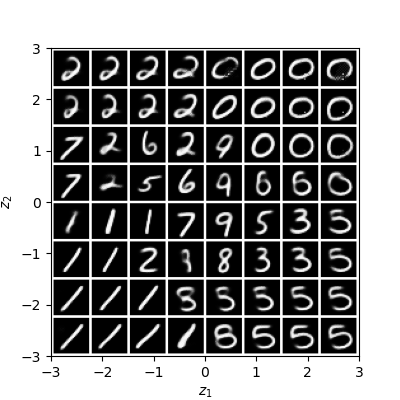
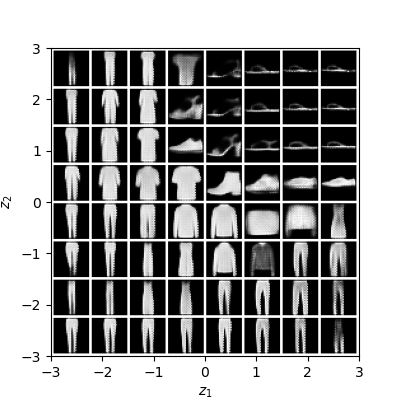
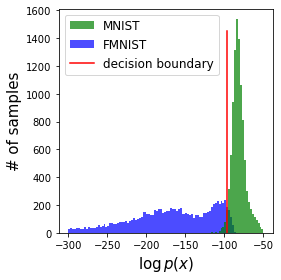
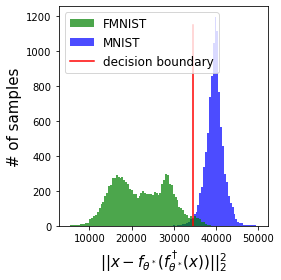
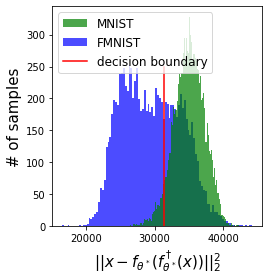
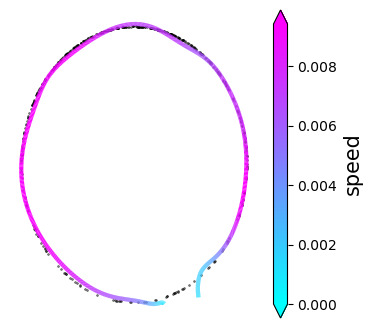
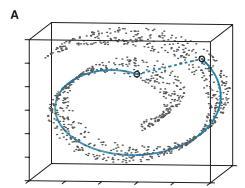
Normalizing flows are inevitable neural networks with tractable change-of-volume terms, which allow optimization of their parameters to be efficiently performed via maximum likelihood. However, data of interest are typically assumed to live in some (often unknown) low-dimensional manifold embedded in a high-dimensional ambient space. The result is a modelling mismatch since -- by construction -- the invertibility requirement implies high-dimensional support of the learned distribution. Injective flows, mappings from low- to high-dimensional spaces, aim to fix this discrepancy by learning distributions on manifolds, but the resulting volume-change term becomes more challenging to evaluate. Current approaches either avoid computing this term entirely using various heuristics, or assume the manifold is known beforehand and therefore are not widely applicable. Instead, we propose two methods to tractably calculate the gradient of this term with respect to the parameters of the model, relying on careful use of automatic differentiation and techniques from numerical linear algebra. Both approaches perform end-to-end nonlinear manifold learning and density estimation for data projected onto this manifold. We study the trade-offs between our proposed methods, empirically verify that we outperform approaches ignoring the volume-change term by more accurately learning manifolds and the corresponding distributions on them, and show promising results on out-of-distribution detection. Our code is available at https://github.com/layer6ai-labs/rectangular-flows.