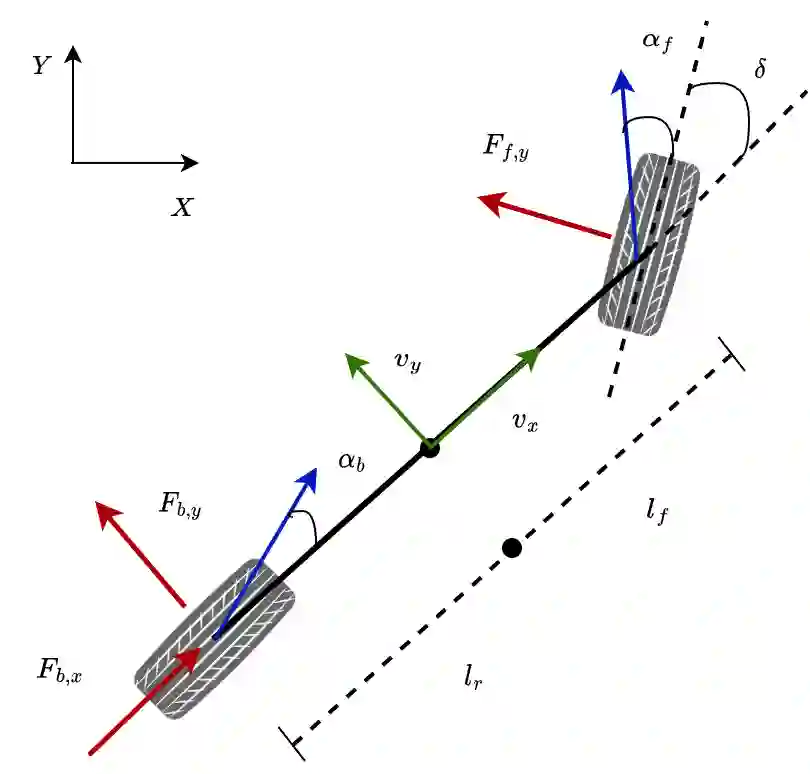
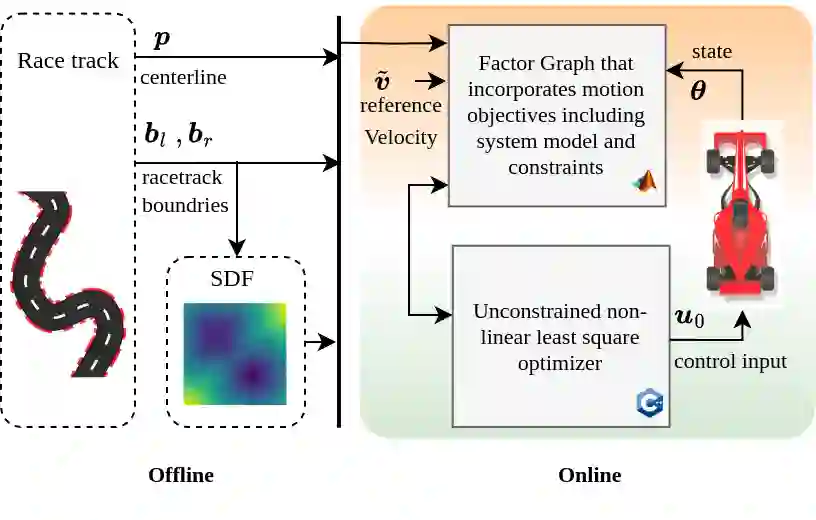
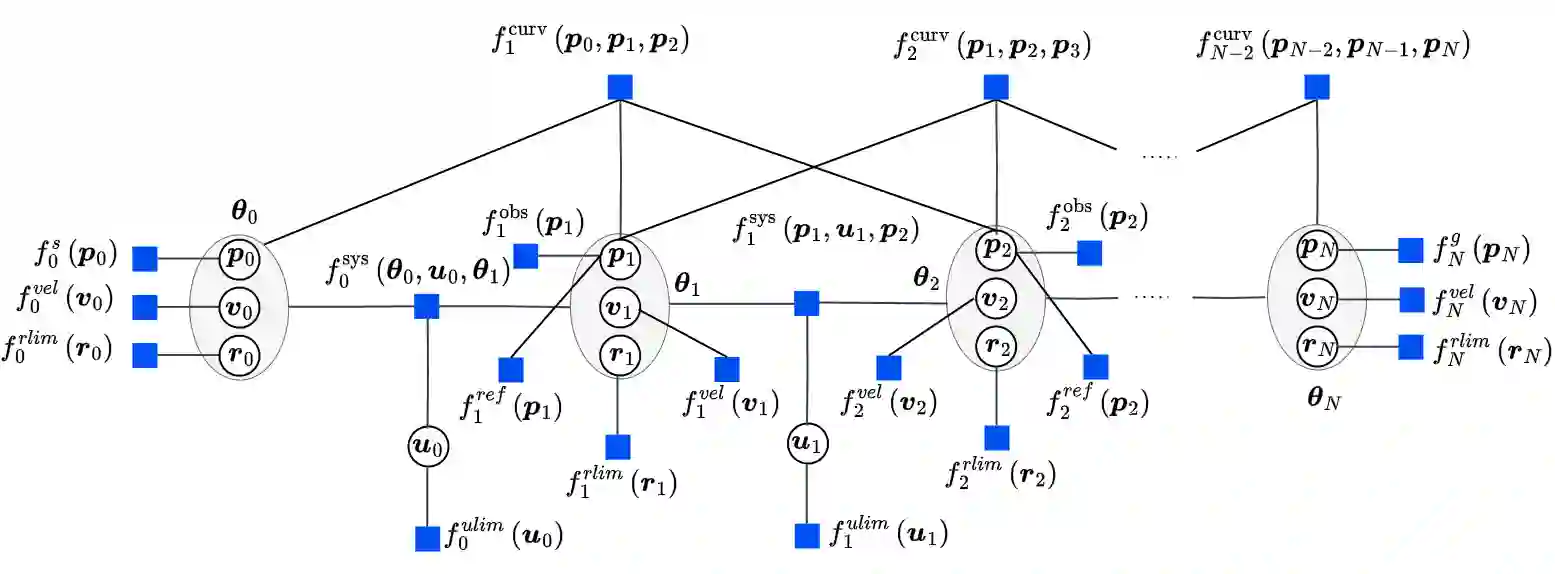
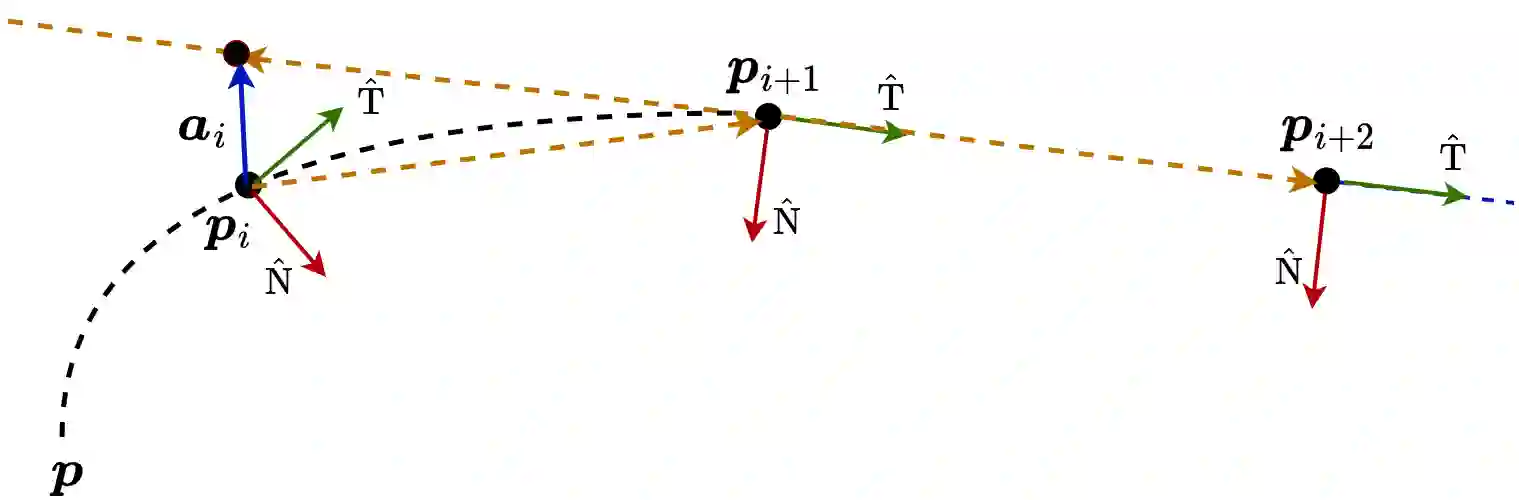
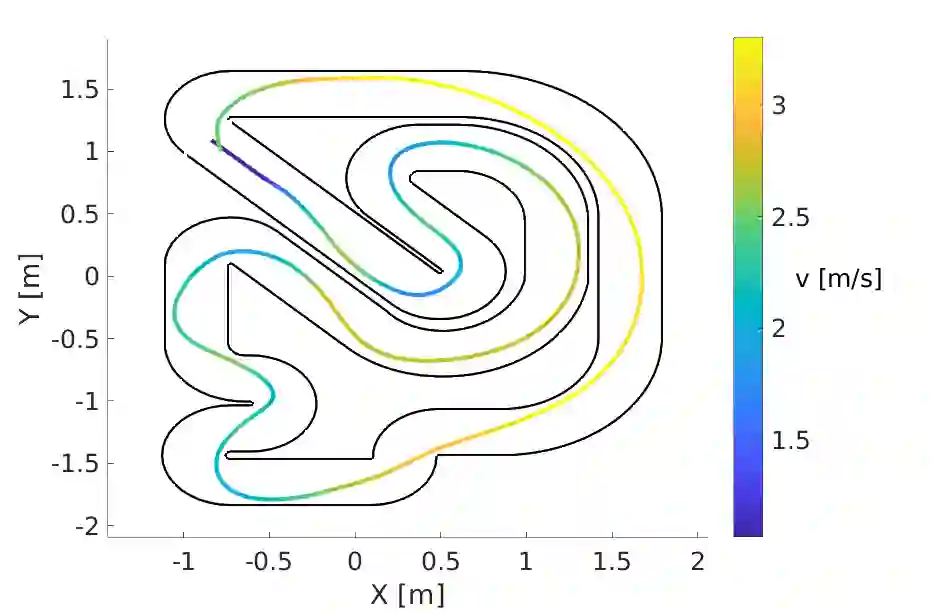
Factor Graph-Based Planning as Inference for Autonomous Vehicle Racing

Factor graph, as a bipartite graphical model, offers a structured representation by revealing local connections among graph nodes. This study explores the utilization of factor graphs in modeling the autonomous racecar planning problem, presenting an alternate perspective to the traditional optimization-based formulation. We model the planning problem as a probabilistic inference over a factor graph, with factor nodes capturing the joint distribution of motion objectives. By leveraging the duality between optimization and inference, a fast solution to the maximum a posteriori estimation of the factor graph is obtained via least-squares optimization. The localized design thinking inherent in this formulation ensures that motion objectives depend on a small subset of variables. We exploit the locality feature of the factor graph structure to integrate the minimum curvature path and local planning computations into a unified algorithm. This diverges from the conventional separation of global and local planning modules, where curvature minimization occurs at the global level. The proposed framework is evaluated through simulation, demonstrating superior cumulative curvature and average speed performance. Furthermore, the results highlight the computational efficiency of our approach. While acknowledging the structural design advantages and computational efficiency of the proposed approach, we also address its limitations and outline potential directions for future research.