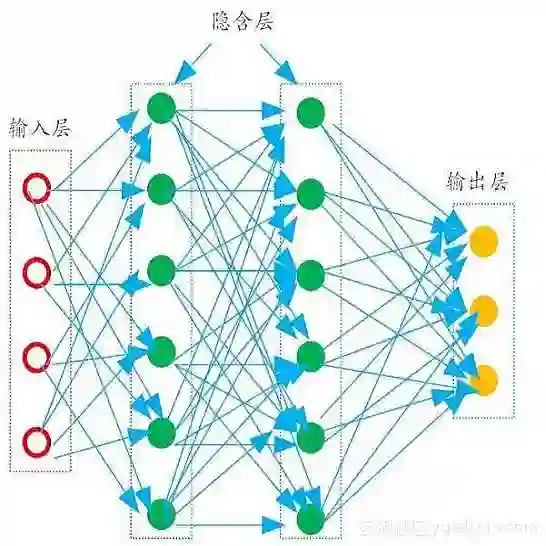
Understanding the fundamental principles behind the massive success of neural networks is one of the most important open questions in deep learning. However, due to the highly complex nature of the problem, progress has been relatively slow. In this note, through the lens of infinite-width networks, a.k.a. neural kernels, we present one such principle resulting from hierarchical localities. It is well-known that the eigenstructure of infinite-width multilayer perceptrons (MLPs) depends solely on the concept frequency, which measures the order of interactions. We show that the topologies from deep convolutional networks (CNNs) restructure the associated eigenspaces into finer subspaces. In addition to frequency, the new structure also depends on the concept space, which measures the spatial distance among nonlinear interaction terms. The resulting fine-grained eigenstructure dramatically improves the network's learnability, empowering them to simultaneously model a much richer class of interactions, including Long-Range-Low-Frequency interactions, Short-Range-High-Frequency interactions, and various interpolations and extrapolations in-between. Additionally, model scaling can improve the resolutions of interpolations and extrapolations and, therefore, the network's learnability. Finally, we prove a sharp characterization of the generalization error for infinite-width CNNs of any depth in the high-dimensional setting. Two corollaries follow: (1) infinite-width deep CNNs can break the curse of dimensionality without losing their expressivity, and (2) scaling improves performance in both the finite and infinite data regimes.
翻译:理解神经网络大规模成功背后的根本原则是深层学习中最重要的开放问题之一。 但是,由于问题高度复杂,进展相对缓慢。 在本说明中,我们通过无边网络的透镜, a.k.a.a.神经内核,提出了由等级位置产生的这样一个原则。众所周知,无限宽度多层感官(MLPs)的叶质结构完全取决于概念频率,它测量了深度互动的顺序。我们表明,深层银度网络(CNNs)的表面结构将相关的静态空间重组为细小的亚空间。除了频率外,新结构还取决于概念空间,它测量非线性互动条件之间的空间。由此形成的精细度结构极大地改善了网络的可学习性,使他们有能力同时模拟一种更丰富的互动,包括长线-线性互动的频率。 短期网络(CNNs) 将相关的静态空间重组为更细小的亚空间。 高端网络的伸缩性能和不同层次的变异性(我们之间) 的变异性、 变变的变的变性、变异性、变异性网络的变的变性、变性、变的变性、变的变的变性、变性、变性、变性、变的变的变的变的变性、变的变的变的变和变的变的变性、变性、变的变的变的变的变的变性、变的变的变性、变的变的变性、变的变和变和变性。