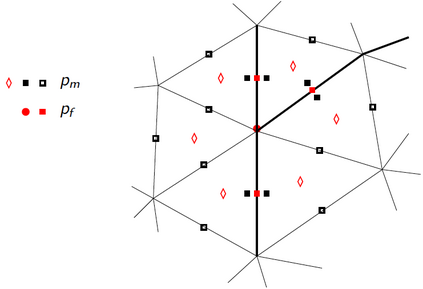
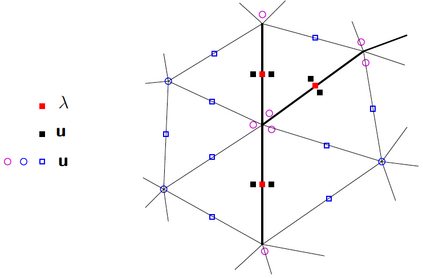
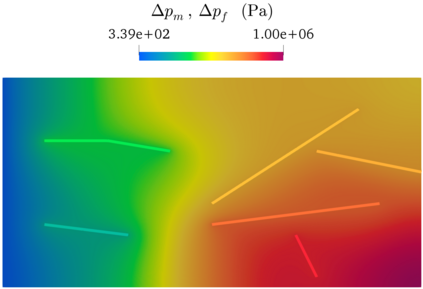
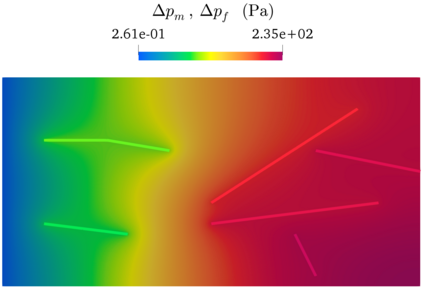
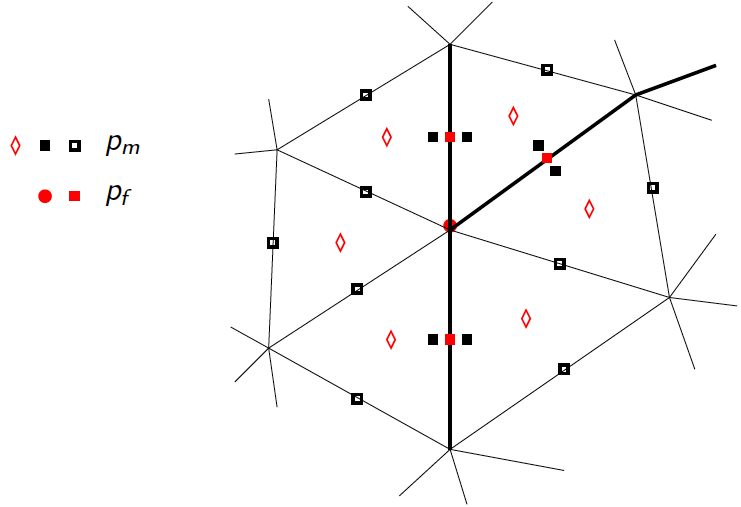
We present a complete numerical analysis for a general discretization of a coupled flow-mechanics model in fractured porous media, considering single-phase flows and including frictionless contact at matrix-fracture interfaces, as well as nonlinear poromechanical coupling. Fractures are described as planar surfaces, yielding the so-called mixed- or hybrid-dimensional models. Small displacements and a linear elastic behavior are considered for the matrix. The model accounts for discontinuous fluid pressures at matrix-fracture interfaces in order to cover a wide range of normal fracture conductivities. The numerical analysis is carried out in the Gradient Discretization framework, encompassing a large family of conforming and nonconforming discretizations. The convergence result also yields, as a by-product, the existence of a weak solution to the continuous model. A numerical experiment in 2D is presented to support the obtained result, employing a Hybrid Finite Volume scheme for the flow and second-order finite elements ($\mathbb P_2$) for the mechanical displacement coupled with face-wise constant ($\mathbb P_0$) Lagrange multipliers on fractures, representing normal stresses, to discretize the contact conditions.
翻译:我们提出了一个完整的数字分析,用于对断裂多孔介质中混合流力机械模型的一般离散,考虑到单相流,包括在矩阵裂缝界面和非线性软质相交界面上无摩擦接触,以及非线性软体机械联结。断裂被描述为平面表面,产生所谓的混合或混合型模型。对矩阵考虑的是小置换和线性弹性行为。矩阵裂裂裂界面中不连续液压模型账户,以覆盖广泛的正常骨折导体。数字分析在梯度裂变框架中进行,包括一个大型的符合和不兼容离散的组合。聚合结果还作为副产品产生连续模型的薄弱溶液。2D的数值实验用于支持所获得的结果,对流动和二级定值元素采用混合的精液量量计划 (\mathbb P_2$),用于与正向常态接触条件相伴的机械离位流和正态离裂变压(Axxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxl)