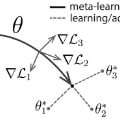
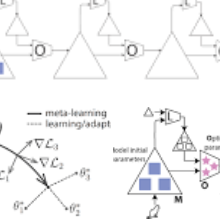
We derive a novel information-theoretic analysis of the generalization property of meta-learning algorithms. Concretely, our analysis proposes a generic understanding of both the conventional learning-to-learn framework and the modern model-agnostic meta-learning (MAML) algorithms. Moreover, we provide a data-dependent generalization bound for a stochastic variant of MAML, which is non-vacuous for deep few-shot learning. As compared to previous bounds that depend on the square norm of gradients, empirical validations on both simulated data and a well-known few-shot benchmark show that our bound is orders of magnitude tighter in most situations.
翻译:具体地说,我们的分析建议对传统的学习到学习的理论框架和现代模型-不可接受的元学习算法进行一般理解。此外,我们提供了一种数据依赖的概括,用于MAML的随机变体,这种变体对于深入的微小的学习来说是不可忽略的。 与以前取决于梯度平方规范的界限相比,模拟数据的经验验证和众所周知的少数点基准都表明,在大多数情况下,我们的界限是更加紧凑的。